量子ビット
状態ベクトル表示
量子ビットの振幅や確率、位相の円表示
量子コンピュータが持つ量子ビット全体の状態を状態ベクトルと呼びます。 状態ベクトルを使えば、量子コンピュータのある時点での状態をベクトル 1 つで表すことができます。 一般にベクトルとは数を並べたものですが、本チュートリアルでは円の並びで状態ベクトルを表現します。 ここでは、状態ベクトルの正しい読み方、特に量子ビットが持つ振幅や確率、位相の概念が円としてどう表されるか詳しく見ていきましょう。
振幅
振幅は、量子ビットの円それぞれの「重み」を表す値です。 重みは量子ビットの測定に関わる値で、測定によって \(|0\rangle\) や \(|1\rangle\) が出る可能性を表すものです。 たとえば確率は、\(|0\rangle\) または \(|1\rangle\) が測定される可能性を直接的に表した値です。 また位相は、\(|0\rangle\) や \(|1\rangle\) が測定される確率を間接的に操作できます位相を参照。。 円それぞれに割り当てられた振幅は、確率と位相の両方を 1 つの値で表します。
振幅と確率の関係
量子ビットを測定した時に 0 または 1 を得る確率は、 \(|0\rangle\) と \(|1\rangle\) それぞれの振幅の 2 乗を計算することによって求められるのでした。 振幅は一般に複素数であるため量子ビットを参照、より正しくは「確率は振幅の大きさある振幅 (複素数) \(\alpha = a + bi\) について、その大きさ \(|\alpha|\) は \(\sqrt{a^2 + b^2}\) で計算できます。確率は振幅の大きさの 2 乗なので、\(| \alpha|^2 = a^2 + b^2\) となります。 (magnitude) の 2 乗」と言えます。 状態ベクトル表示では、青く塗りつぶされた円の半径は振幅の大きさを表すので、その面積 (半径 x 半径 x π) はその確率に正比例します。 状態ベクトルの円にマウスオーバーすると、それぞれの振幅と確率をポップアップ表示します。 下の円それぞれにマウスオーバーして、たしかに振幅の大きさの 2 乗が確率と等しくなっていることを確認しましょう。
振幅と位相の関係
状態ベクトルの円それぞれの位相は、複素数である振幅の偏角を表します。 偏角とは振幅の値 (複素数) \(\alpha = a + bi\) の \(a\) と \(b\) によって決まる次の角度です。
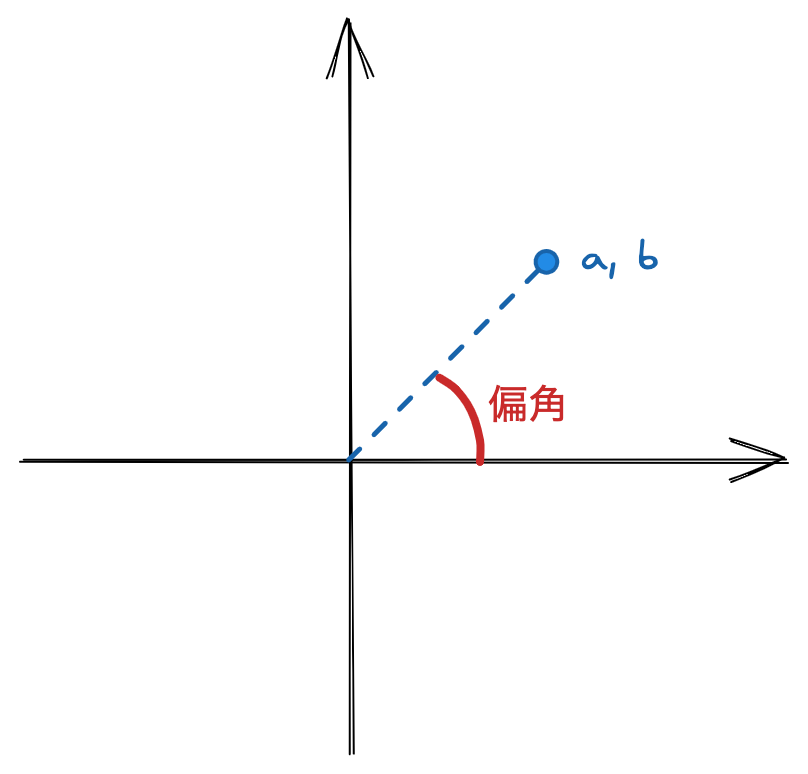
たとえば下の π/4 の \(|1\rangle\) のポップアップを見ると、振幅が \(0.5 + 0.5i\) となっています。 \(a\) と \(b\) はそれぞれ \(0.5\) と等しいので、上の図で考えると偏角は確かに π/4 (45°) となります。 余裕のある人は、ほかの偏角と振幅も確認してみましょう。
| 偏角 | 円表示 |
|---|---|
| π/4 |
|
| π/2 |
|
| π |
|
| 3π/2 |
|
まとめ
状態ベクトル表示から読み取れる振幅と確率、位相の関係を紹介しました。 測定結果に影響する「円の重み」が振幅であり、振幅から確率と位相という独立した 2 つのプロパティが得られます。 状態ベクトル表示は確率を青色の円の半径、位相を時計の針の角度として表示します。
