周期 \(r\) を求める

周期 \(r\) を求めるには、パターンを取り出すツールである QFT を使います。 たとえば \(N = 15\), \(a = 2\) の場合、後で実際に実行して確認しますが、\(2^x\,mod(15)\) の値を持つ状態ベクトルに QFT を適用し測定すると、次のような確率のピークがいくつか得られます。

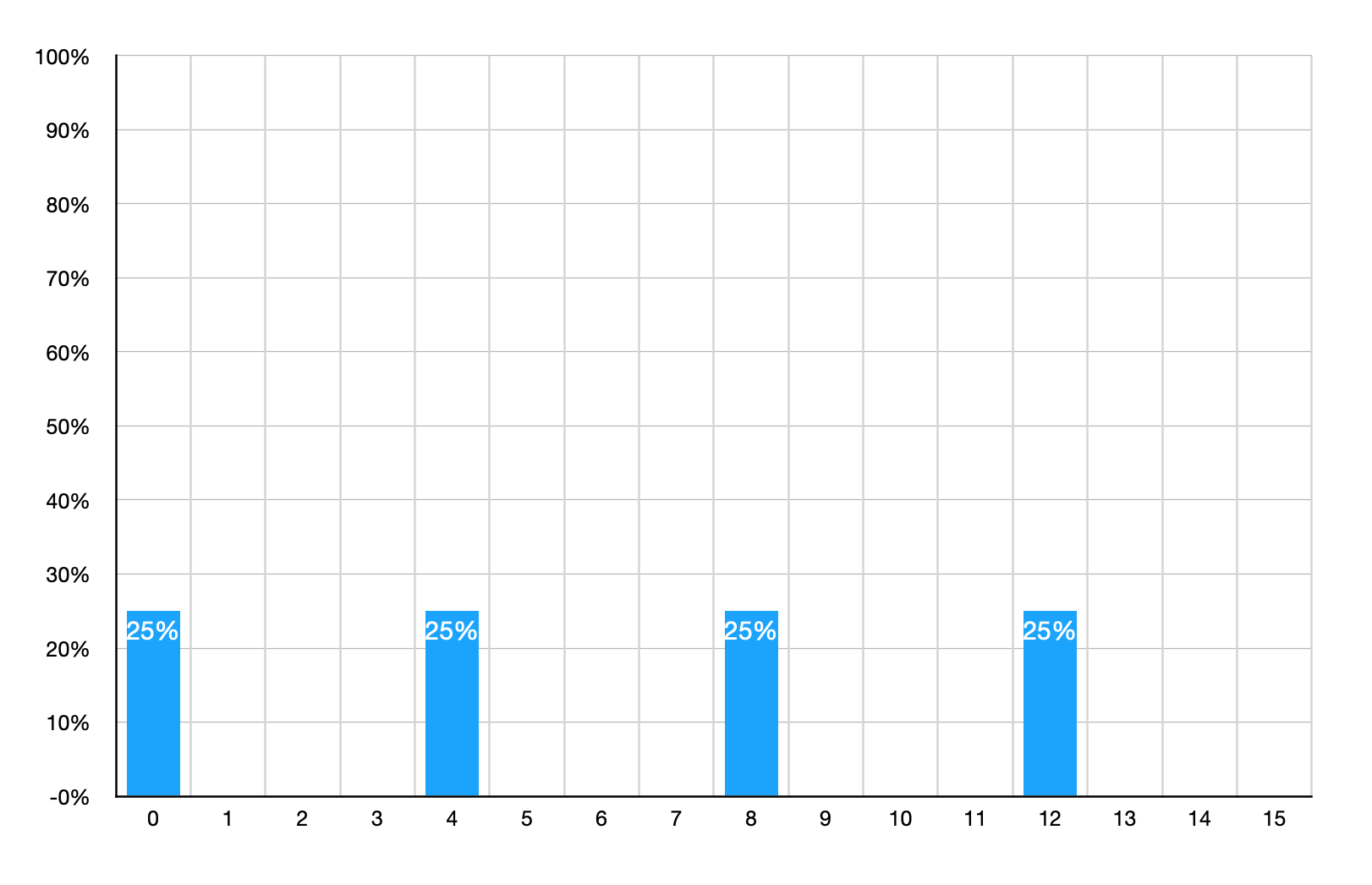
QFT で得られる確率のピークは、周期 \(r\) のヒントを与えるものです。 ピークの数はちょうど周期 \(r = 4\) と同じになり、0 から始まって等間隔に並びます。

これを測定すると 0, 4, 8, 12 のうち 1 つだけがランダムに手に入るので、測定結果からは直接周期 \(r\) は得られないことに注意してください。 しかし、これらは等間隔であること、また x の範囲は 0 〜 15 であることをうまく使うと、周期 \(r\) の候補が計算から推定できます。

この \(r\) の候補を出すアルゴリズムを連分数アルゴリズムと呼びます。 詳細は省きますが興味のある読者は、Qiskit チュートリアル「ショアのアルゴリズム」を参照してください。https://qiskit.org/textbook/ja/ch-algorithms/shor.html これは古典コンピュータで計算でき、\(N = 15\), \(a = 2\) の場合には \(r\) の候補として 4 と 8 が得られます。

あとは \(r = 4, 8\) それぞれの候補について \(gcd(N, a^{r/2} + 1)\) と \(gcd(N, a^{r/2} - 1)\) を計算して、それぞれが \(N = 15\) の因数になっているかチェックします。これらは古典コンピュータで簡単にでき、 \(r = 4\) の場合因数 3 と 5 がみつかるので、計算は終了です。