別問題に帰着する

ショアの因数分解アルゴリズムは、量子コンピュータが得意とする計算のうち最も有名なものの 1 つです。 はじめにで述べたように、因数分解が高速にできると、公開鍵暗号を現実的な時間のうちに解くことができます。 公開鍵暗号はインターネット通信やビットコイン技術等の拠り所であるため、これが解けてしまうというインパクトは相当なものです。

ショアの因数分解アルゴリズムはどれほど速いのでしょうか。 古典の因数分解アルゴリズムである「一般数体ふるい法」の実行時間は、因数分解したい数が大きくなるにつれて指数関数的に増えます。 一方でショアのアルゴリズムは、多項式時間に留まります。 分かりやすく具体的な値で言うと、1024 ビットの整数を因数分解するのに必要な計算量は、古典コンピュータ (一般数体ふるい法) で \(O(10^{278})\) です。 これに対して、ショアのアルゴリズムは \(O(10^{61})\) となり、\(10^{278} \rightarrow 10^{61}\) と計算量を大幅に減らせます。

因数分解を別問題として解く

因数分解のような整数問題の多くは、より解きやすい別問題に帰着させて解くことができます。 ショアのアルゴリズムでは、因数分解を次の別問題に帰着させます (一見むずかしそうな数式が出てきますが、すぐ後に具体例で説明するので安心してください)。

分かりやすくするために、\(a\) や \(N\) に具体的な値を入れて関数 \(f(x)\) がどう動くか見ていきましょう。 因数分解したい数 \(N\) を 15 とします。 \(a\) はとりあえず \(N\) より小さい整数なら何でも良いので、ここでは 2 とします。すると、\(f(x)\) は次のように書き直せます。

\(f(x) = 2^x mod(15)\)

この関数をグラフにして見てみましょう。

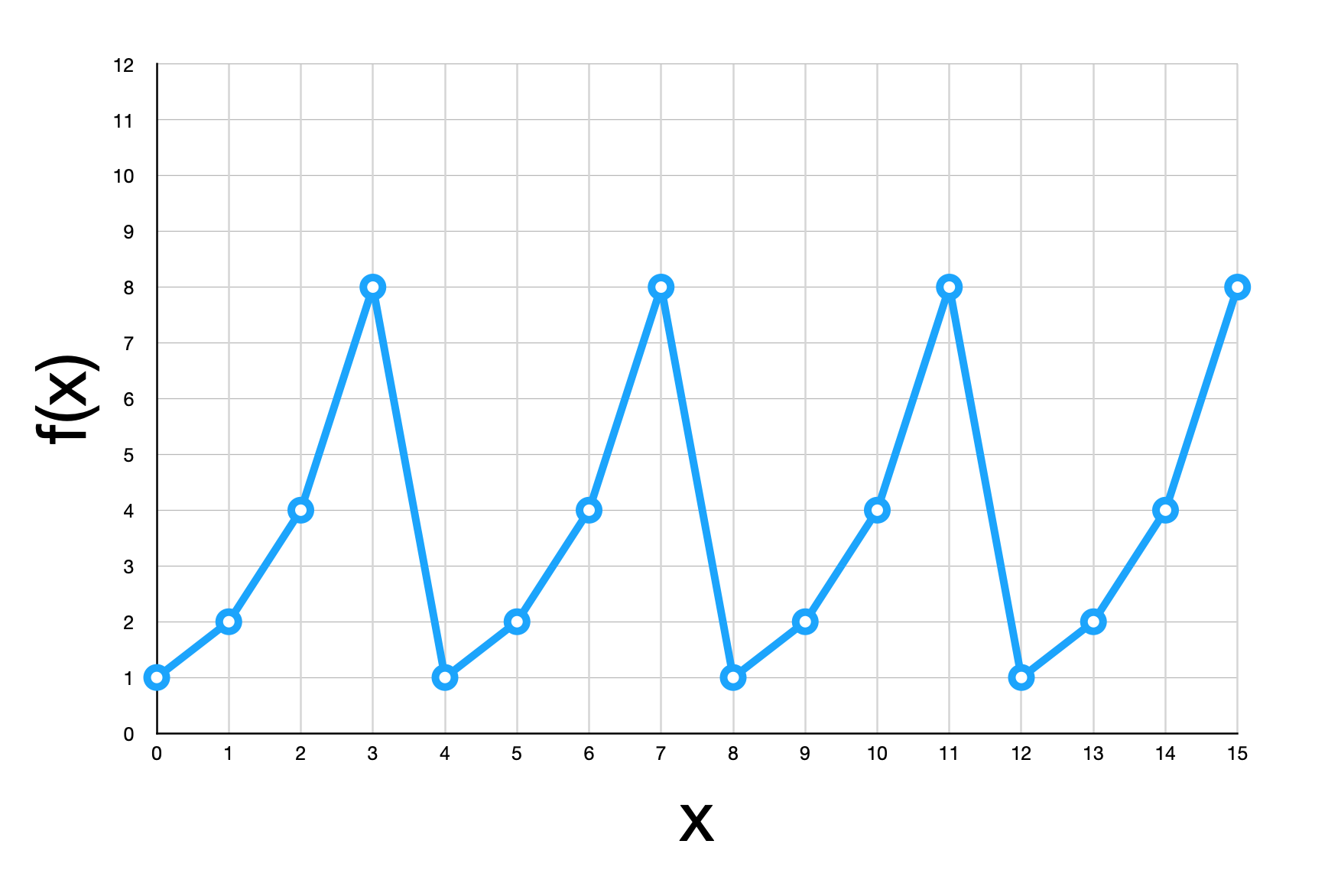
グラフから一目瞭然のとおり、この関数はたしかに周期関数になっています。 そして x が 4 増えるごとにまったく同じ形の波が現れるので、反復周期 \(r\) は 4 です。

反復周期 \(r = 4\) が求まれば、\(N\) の因数はそれぞれ次の単純な計算で求まります。

• \(gcd(N, a^{r/2} + 1)\)
• \(gcd(N, a^{r/2} - 1)\)

ここで出てくる \(gcd\) とは最大公約数 (greatest common divisor) の略で、古典コンピュータでも高速に計算できる処理です。 たとえば \(N = 15\) の場合で具体的に計算してみると、\(a = 2\), 周期 \(r = 4\) をこの式に入れてみると、

• \(gcd(N, a^{r/2} + 1) = gcd(15, 2^{4/2} + 1) = gcd(15, 5) = 5\)
• \(gcd(N, a^{r/2} - 1) = gcd(15, a^{4/2} - 1) = gcd(15, 3) = 3\)

たしかに \(15 = 5 \times 3\) が求まりました!

古典コンピュータでショアのアルゴリズムを実行すると?

もしショアのアルゴリズムを古典コンピュータで実行すると、計算量はどうなるでしょうか。 ショアのアルゴリズムの核心は、\(f(x)\) の反復周期 \(r\) を求める部分でした。 古典コンピュータで周期を求めるには、\(f(x)\) の同じ値 (1, 2, 4, 8 など) が出てくる間隔を求めることで周期が求まります。 これは、\(f(x)\) の 1 つの周期には同じ値が 1 度しか出てこないことが数学的に分かっているためです。 これを使えばたとえば、\(x\) を 1 つずつ増やしながら \(f(x)\) が再び 1 となる点の \(x\) を求めることで \(r\) も求まります。

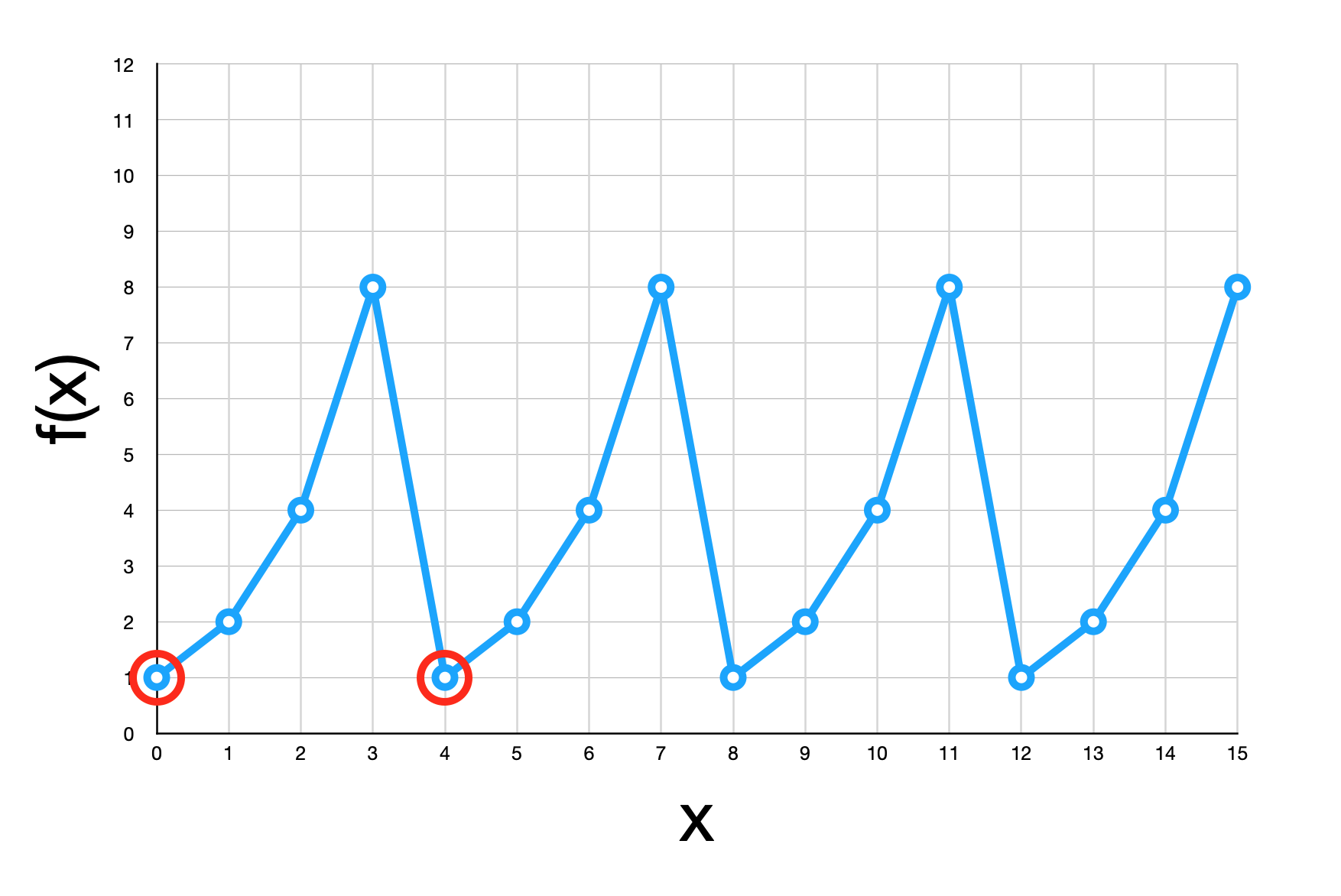
問題は、\(N\) のビット数が増えるにつれて反復周期 \(r\) が指数関数的に増えることです。 このため、古典コンピュータではショアのアルゴリズムを使ってもやはり指数時間かかってしまいます。

まとめ

ショアの因数分解アルゴリズムは、関数 \(f(x) = a^x mod(N)\) の反復周期を求めるという別問題を解くことで因数を求めます。 この周期を求める計算は、古典コンピュータでは指数時間が必要なため、量子コンピュータを使います。 求めた周期を使って古典コンピュータで gcd を計算することで、\(N\) の因数が求まります。