位相論理演算

位相論理演算は、論理演算の結果を振幅の大きさではなく位相に出力するテクニックです。 位相バージョンの AND, OR といった論理演算は、入力として論理演算と同じく振幅を取り、出力として位相のみを変化させます。 位相は では直接読み出せないため隠れた情報ですが、いくつかの計算で位相の値を利用できます。

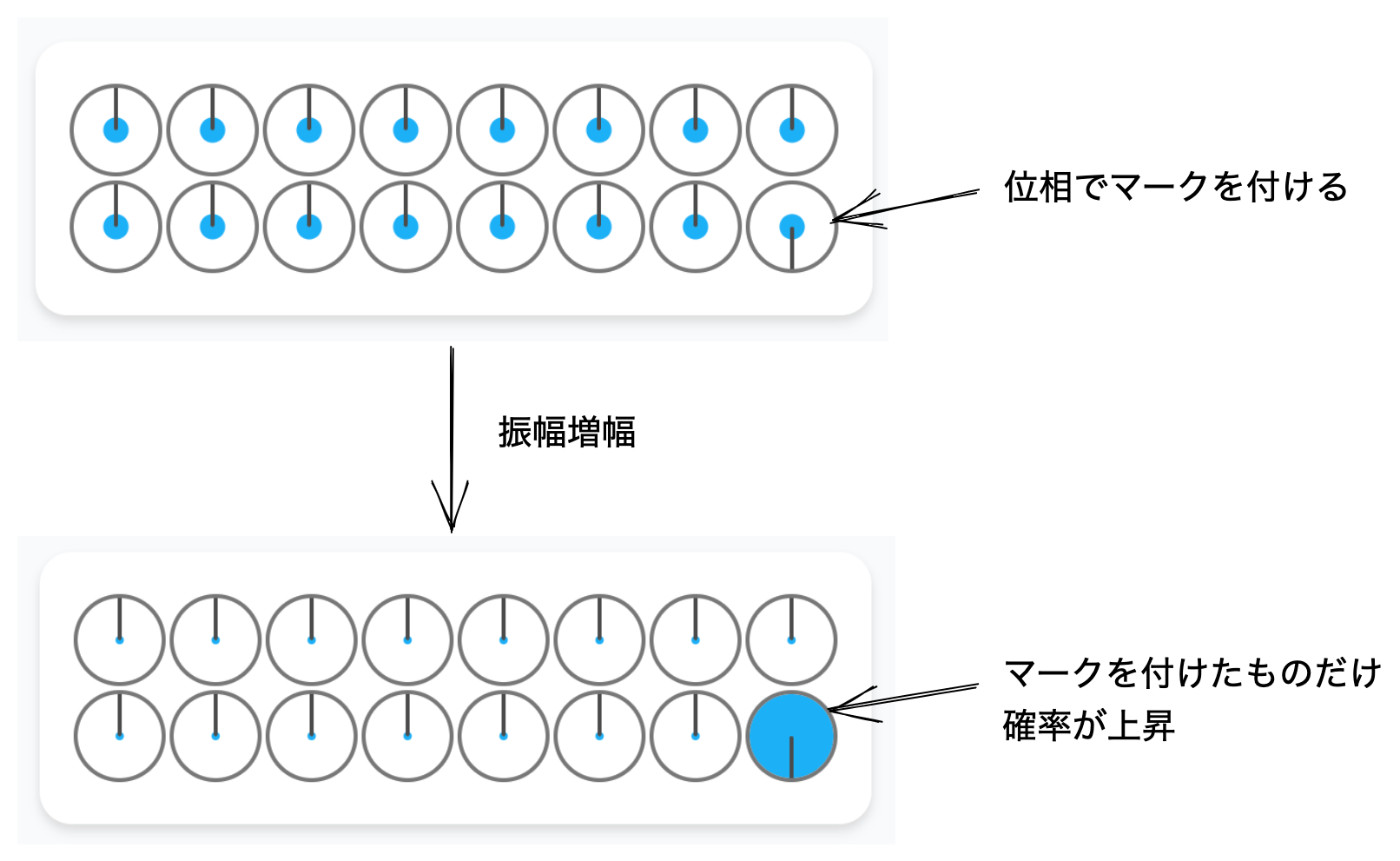
たとえば後で紹介する振幅増幅は、位相を使った強力なテクニックの 1 つです。 以下のように位相論理演算によってある振幅の位相を反転 (πの回転) させ「マーク」をつけます。 振幅増幅は、各振幅の位相差を振幅の大きさの差に変換します。 これによって、マークを付けた値の確率だけを上昇させ、ほかの確率を下降させることによって、 で読み出しやすくします。

位相論理 NOT (pNOT)

位相論理 NOT は 1 つの入力ビットの振幅のうち \(|0\rangle\) の位相を反転します。 これは普通の論理演算で 0 を NOT で反転すると 1 (true) になるためです。 \(|0\rangle\), \(|1\rangle\) および重ね合わせ状態に pNOT を適用した結果は次のようになります論理 NOT と区別するために、pNOT という記号を導入します。p は phase (位相) を表しています。以降では同様に、pAND, pOR, ... のように p で区別していきます。。

pNOT 回路は次のように と を組合わせて作ることができます。

位相論理 AND (pAND)

位相論理 AND は、2 つの入力ビット a, b を取り \(|3\rangle\) の位相を反転させます。 これは、普通の論理演算で a と b がそれぞれ 1 (= 十進数で 3) のときのみ a AND b = 1 になるためです。

pAND 回路は次のように CPHASEπ 回転の を条件付きで実行するもの。 2 つで略記できる。詳しくはCPHASE ゲート参照 一個で表せます。

位相論理 OR (pOR)

位相論理 OR は、2 つの入力ビット a, b を取り \(|1\rangle\), \(|2\rangle\), \(|3\rangle\) の位相を反転させます。 これは 1, 2, 3 を二進数で表した 01, 10, 11 のそれぞれ上下 2 ビット a, b について、a OR b = 1 が成り立つためです。

pOR 回路は次のように π 回転の と CPHASE を組合わせて作ることができます。

位相論理 NAND (pNAND)

位相論理 NAND は、2 つの入力ビット a, b を取り \(|0\rangle\), \(|1\rangle\), \(|2\rangle\) の位相を反転させます。 こうなる理由は pAND の考え方と同じく、0, 1, 2 の上下 2 ビット a, b について a NAND b = 1 が成り立つためです。

pNAND 回路は以下のように作ることができます。

位相論理 NOR (pNOR)

位相論理 NOR は 2 つの入力ビット a, b を取り \(|0\rangle\) の位相を反転させます。 これは「NOR = OR の結果を NOT で反転させたもの」と考えると分かりやすいでしょう。

pNOR 回路は以下のように作ることができます。

位相論理 XOR (pXOR)

位相論理 NOR は 2 つの入力ビット a, b を取り, a XOR b の結果として \(|1\rangle\) と \(|2\rangle\) の位相を反転させます。

pXOR 回路は他の位相論理回路と異なり、入力 a, b のほかに一時ビット c を必要とします。 c は pXOR 計算後にアンコンピュートされ \(|0\rangle\) に戻ります。

まとめ

位相論理演算は入力として振幅を取り、出力として位相に結果を書き込みます。 このとき振幅の大きさは変化せず、結果が 1 となる振幅の位相のみが反転する点がポイントです。 結果を位相に書き込む目的は、振幅増幅のプロセスを通じて振幅の大きさを増幅することで、 による測定で答を取り出しやすくすることです。