論理演算
重ね合わせ上での論理演算
論理演算を振幅として出力
前節で見た論理演算を組合わせて、結果がどのように出力されるか見てみましょう。 今回は、入力として a,
b, c 3 ビットの均一な重ね合わせを取ります。 a, b, c はそれぞれ量子ビット 1, 2, 3 に割り当てます。
その上で、論理式 a OR (NOT b) AND c一般的なプログラミング言語の論理式では a || !b && c と書けます。 を計算します。
答合わせ用に、真理値表を書いてすべての場合を調べてみましょう。
a OR (NOT b) AND c が 1 となるのは、(a, b, c) が (1, 0, 0) または (1, 0, 1) または
(1, 1, 1) の時です。 これはそれぞれ \(|4\rangle\), \(|5\rangle\), \(|7\rangle\) に対応します。
つまり答は 4, 5, 7 の 3 つです。
| a | b | c | a OR (NOT b) |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
a OR (NOT b) AND c を前回の量子論理ゲートを使って実装したものが以下になります。 NOT
と OR 演算にはそれぞれ出力用のビットが必要なので、NOT b の結果を d (ビット 4), a OR d
の結果を e (ビット 5) に出力しています。 また、最後に結果 e 以外のビット (a, b, c, d)
をアンコンピューテーションで戻しておきます。
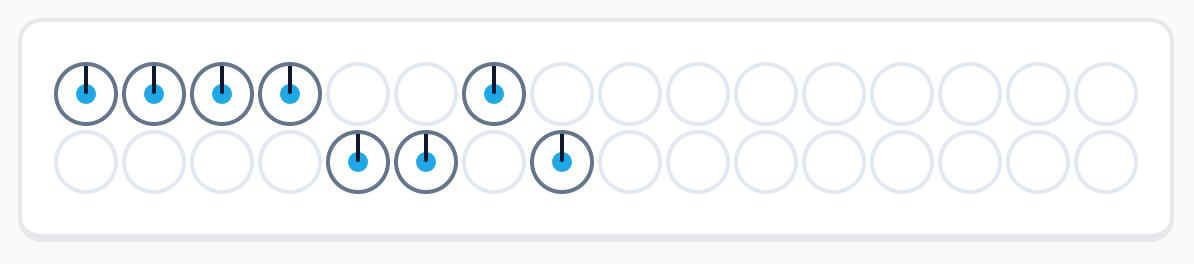
この回路の実行結果は以下のようになります。答のビット e (5 ビット目) が 1 である振幅が
a OR (NOT b) AND c を満たす a, b, c を表し、 下の行の \(|10100\rangle\), \(|10101\rangle\), \(|10111\rangle\) がこれにあたります。d, e の上位 2 ビットを無視すると、確かに 4, 5, 7
が答として得られていることが分かります。
答の読み出し
この結果は量子コンピュータから効率的に読み出すことができません。
なぜならば、正しい答とそうでないものが同じ確率で重ね合わされているため、a OR (NOT b) AND c
を満たしていない (= 最上位ビット e が 1 でない) 振幅のほうが確率的に多く測定されてしまうためです。
今回のように 3 ビットなら答は 8 通り (それぞれの確率は 12.5%) なので、何百回か測定すれば 4, 5, 7
を読み出すことはできます。
しかし、ビット数が増えるにつれひとつひとつの答の確率が指数的に小さくなるので、必要な測定回数が大幅に増えてしまいます。
算術演算でも見てきたように、これは重ね合わせ上で計算をする場合に必ず出てくる問題です。 重ね合わせで並列計算ができても、その結果を読み出せなければ意味がありません。
そこで、次の回では量子論理ゲートを少し改造し、うまく読み出せるような形に出力する方法を見ていきます。
