確率的ビット

量子コンピュータの計算結果を取り出すには、確率に基づいた測定という操作があるのでしたQPU は何が得意? を参照。。 序盤でいきなり迷子にならないためにも、まずは簡単な確率の世界に慣れておく必要があります。

この節では、現在のコンピュータが持つビットをおさらいした後、確率と確率的ビットを学びます。 確率的ビットは量子コンピュータの量子ビットによく似ているので、確率的ビットを通して量子ビットの重要な側面を理解できます。 ここでは、確率的ビットの状態はどんなものか、また測定によって確率的ビットからどのように情報を取り出せるかを見ていきます。

古典ビット

ご存知のように、従来のビット (古典ビット量子力学と古典力学との対比から、量子コンピュータのビットを量子ビットと呼ぶときは、現在のコンピュータのビットを古典ビットと呼びます。とも呼ぶ) は 0 または 1 のどちらかの値をとります。ごく当たり前のことですが、古典ビットから取り出せる値は 0 か 1 のみです。 また計算中のその中身 (状態) も常に 0 か 1 です。

確率

確率とは「元旦には 10% の確率で雪が降る」とか「80% の確率で日本列島に台風が上陸する」などのように、あるイベントが起こる可能性を数値化したものです。 確実に発生するイベントなら 100%、絶対に発生しないイベントなら 0% の確率を持ちます。

確率の例として、コイントスを考えてみましょう。 コインを投げてそれを見ずに手で覆うと、手の中ではコインが「表」または「裏」の 2 通りのイベントが発生します。 偏りのないコインならば、それぞれのイベントの確率は 50% ずつです。 また、表の出やすいコイン (表 60.8%、裏 39.2%) や両面が裏のインチキコイン (表: 0%、裏: 100%) など、無限のバリエーションが存在します。

表と裏の確率を足すと必ず 100% になる確率論では、起こりうるすべてのイベントの確率を足すと 100% になります。ことを考えると、表と裏になる確率すべての組合わせを次のグラフに図式化できます。 横軸は表の出る確率 (0〜100%)、縦軸は裏の出る確率 (0〜100%) です。 あらゆるコインの性質を表と裏が出る確率で特徴付けしたとき、任意のコインはこの線分上のどれか 1 点として表せます。

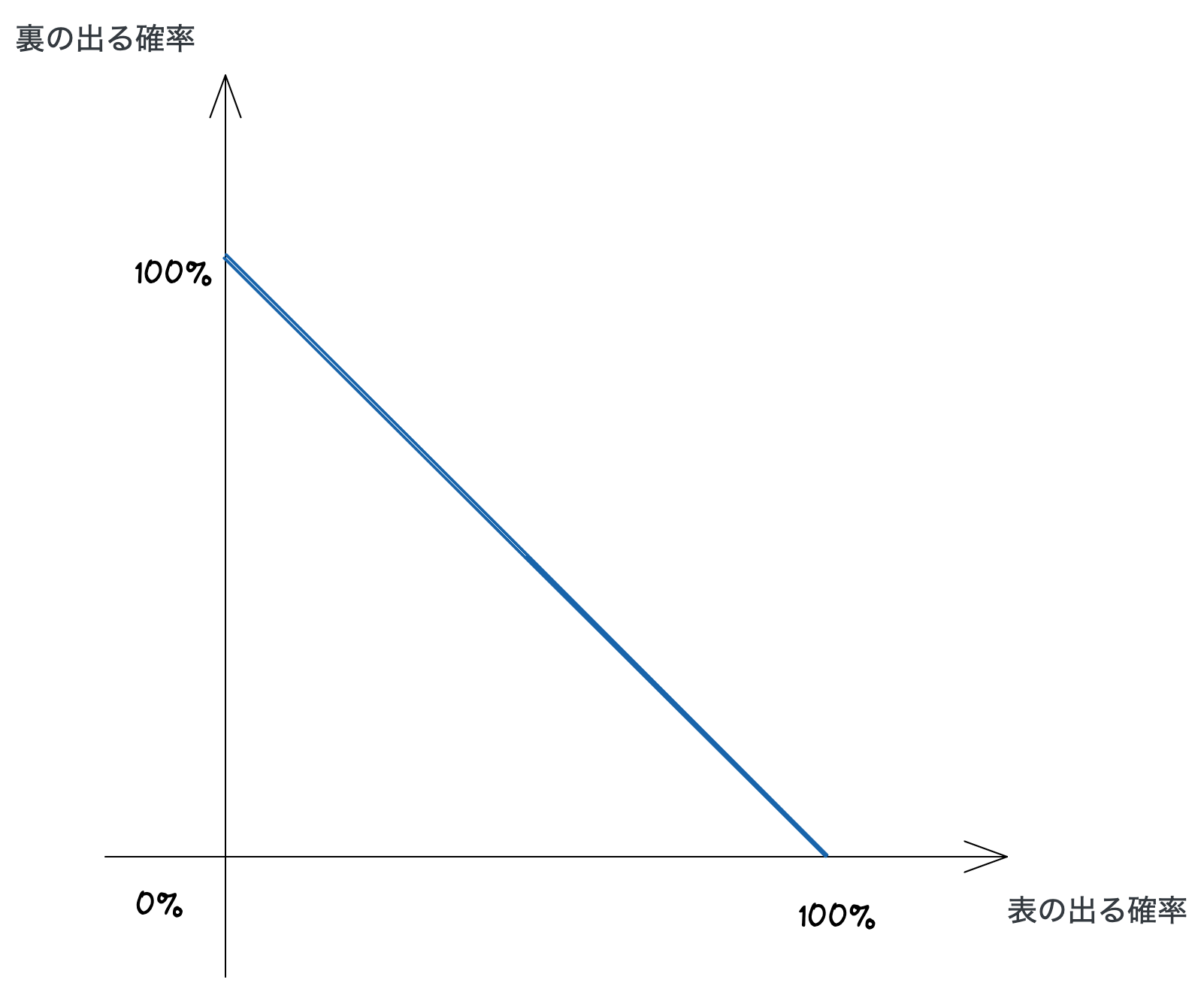
確率的ビット

確率的ビットは、コイントスと同じ確率的な性質を持っています。 計算中の確率的ビットの状態は、コインが手の中にあり表か裏かまだ分かっていない状態と同じと考えられます。 コインの表を値 0、コインの裏を値 1 とすると、確率的ビットはたとえば「60% の確率で 0、40% の確率で 1」などという状態を取ることができます。

計算後、値を取り出す操作 (測定) をした後の確率的ビットは、コインの表か裏かが定まった状態に対応します。 つまり、値を取り出した時点で確率は消え 0 か 1 かが確定するので、古典ビットとまったく見分けがつきません。

こうした確率的な情報はいったいコンピュータの計算に使えるのでしょうか? 古典ビットの値 0 と 1 は確定した値を表しているのに対し、確率的ビットはおおよその知識 (または知識の欠如) を表しているので、あまり役に立たないと思うかもしれません。 確率ビットの利点は、部分的な知識をより正確に表現できることです。 もし何かが完全に分かっていないのであれば、計算をあきらめるのではなくそれを認め、確率のまま計算を進めてしまおうというのが確率的ビットの考えかたです。

重ね合わせはなぜ強力?

確率的ビットの確率的な 0 と 1 の状態を重ね合わせ状態と言います。 0 または 1 が起こる 2 つの確率を重ね合わせ、「0 が 60%、1 が40%」という 1 つの状態として扱うイメージです。 重ね合わせは量子コンピュータが強力である 1 つの理由としてよく挙げられますが、それはなぜでしょうか?

直感的に納得する方法の 1 つは、先ほどのグラフ上で古典ビットと確率的ビットを直接比べてみることです。 古典ビットは常に 0 または 1 の状態しか取りませんから、先程のグラフ上に表すと古典ビットの取りうる状態は 2 点になります。

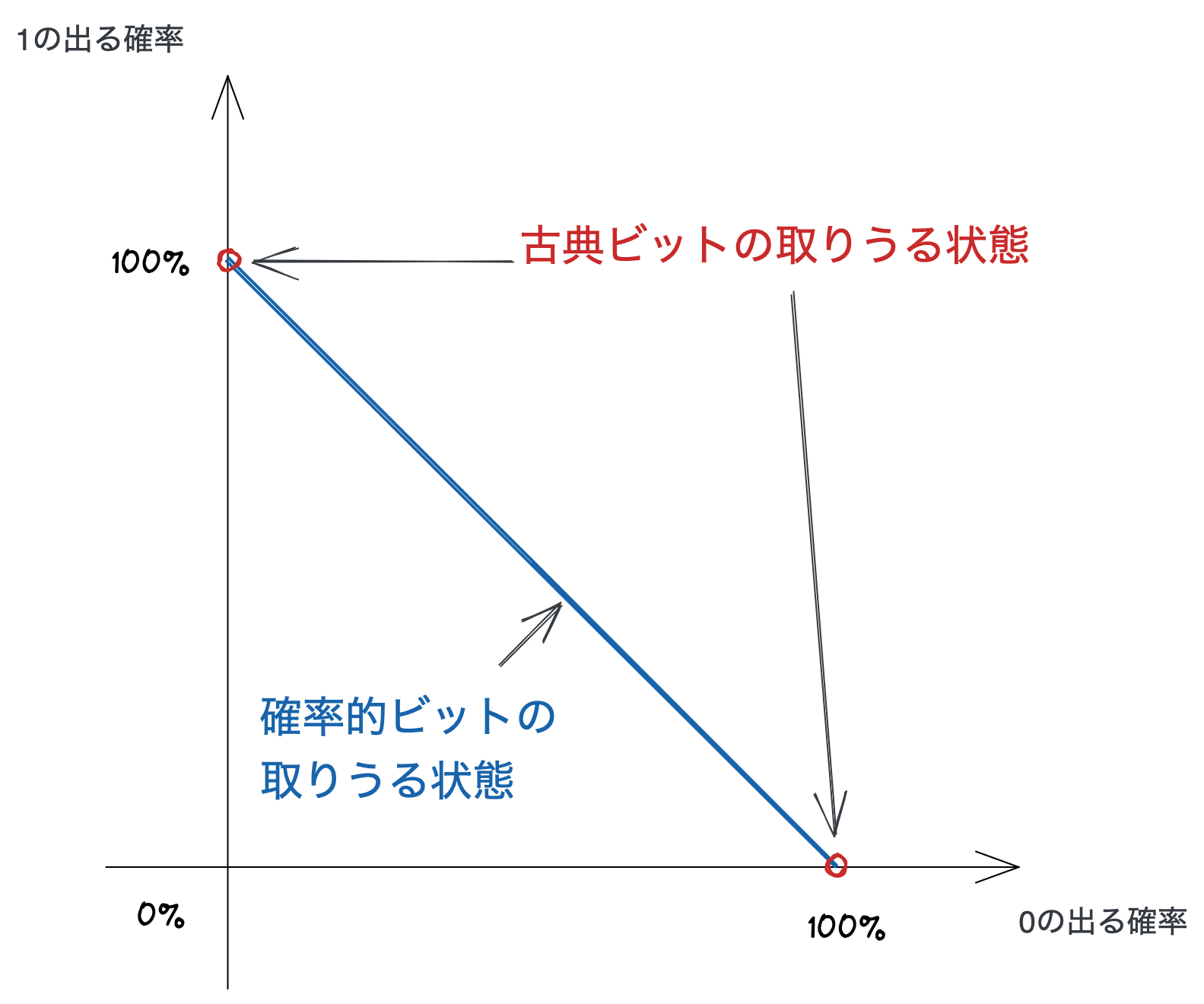
一方で、確率的ビットは線分上のすべての点、つまり無限個の状態を持ちえるのでした。 このように取りうる状態の数で比較すると、古典ビットは 2 個であるのに対して確率的ビットは無限個なので、確率的ビットのほうが (なんとなく) 強力に見えます。

またはこう考えることもできます。 確率的ビットの状態は「0 が 0.11001001011%、1 が 99.88998998989%」のようにいくらでも細かくセットできます。 ここで 0 の確率の少数点以下を 2 進数と見て、そこにすべての Wikipedia の記事と YouTube の全動画データ、そしてインターネットでみつかるすべての猫画像を 2 進数として埋め込みます。 それはなんと、確率的ビットたった 1 個に超巨大なデータを埋め込めることにほかなりません!

…実際に埋め込めたとしても、測定によって 0 または 1 しか取り出せないなら、確率に乗せたデータは消えてしまうのではないでしょうか? たしかにその通りですが、測定前なら確率の値を計算データとして使えます。 このように、膨大なデータでも確率の形にエンコードして持つことができ、それを計算データとして使える量子機械学習アルゴリズムでは、膨大なデータをこのように確率として量子ビットに埋め込むことで量子コンピュータに入力し計算します。のが確率的ビットの強みです。