演算ペア

前項では、複数量子ビットに対して QPU 命令を作用させるときの演算ペアの考え方を紹介しました。 \(n\) 番目のビットにゲートを置くと \(2^{n - 1}\) 離れた円同士がペアとなるのでした。 なぜこのようになるのでしょうか?

3 量子ビットの回路を例に説明します。 H ゲートなどの QPU 命令は 1 ビット目、2 ビット目、などビットを対象に演算します。 演算ペアのルールは、状態ベクトルの円の番号を 2 進数としてビット単位で考えると分かりやすくなります。 右を最下位ビットとする 2 進数で円の番号を表すと、次のようになります。

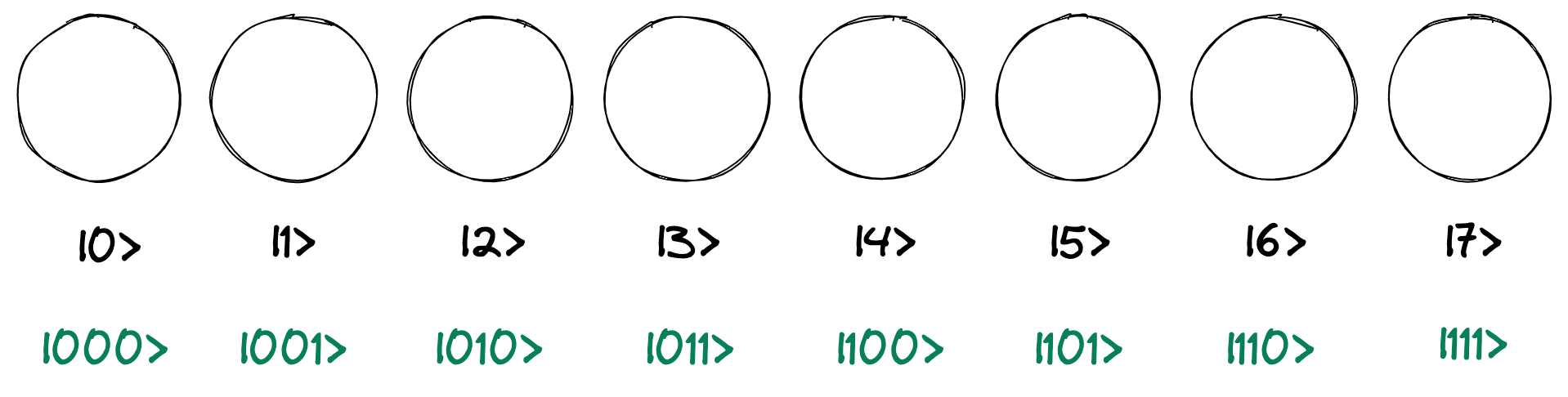
ここで、1 ビット目に QPU 命令を適用する場合の演算ペアを考えます。 1 ビット目に適用する場合、2 進数表記で右から 1 ビット目だけが異なる円でペアを作ります。 たとえば \(|0\rangle\) と \(|1\rangle\) はそれぞれ 2 進数では \(|000\rangle\) と \(|001\rangle\) で右から 1 ビット目だけが異なるので、 これをペアとします。2 進数で右から 1 ビット目だけが異なるということは、10 進数では \(2^0 = 1\) だけ離れていることになります。 よって、隣同士の円がペアとなります。

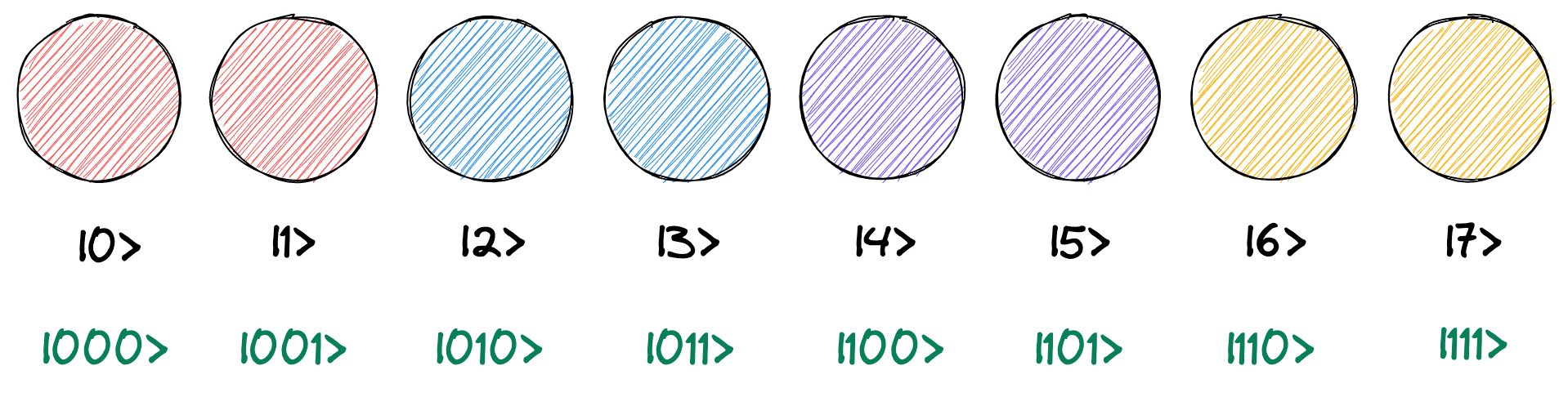
同様に、2 ビット目に QPU 命令を適用する場合は、2 進数表記で右から 2 ビット目だけが異なる円でペアを作ります。 これは 10 進数では \(2^1 = 2\) だけ離れていることになります。 よって、2 つ離れている円同士がペアとなります。

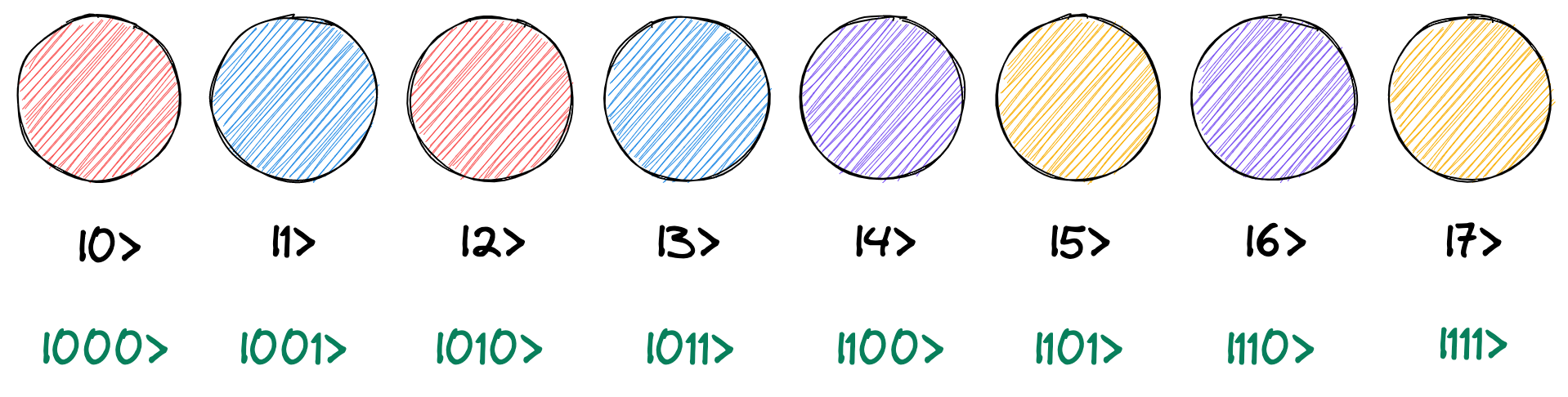
まったく同様に、3 ビット目に QPU 命令を適用する場合は、2 進数表記で右から 3 ビット目だけが異なる円でペアを作ります。 これは 10 進数では \(2^2 = 4\) だけ離れていることになるので、4 つ離れている円同士がペアとなります。

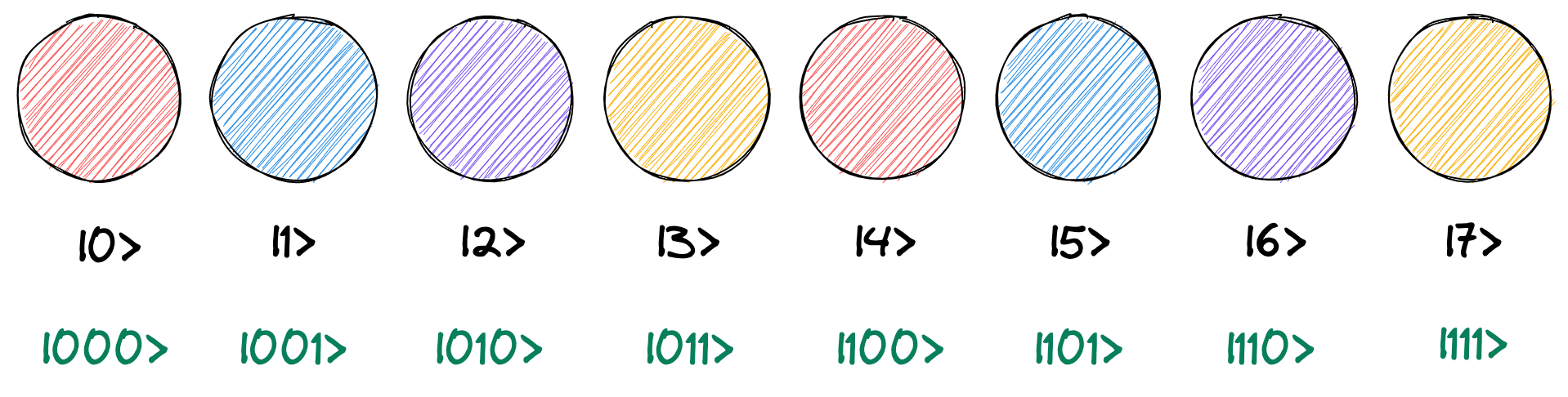
以上をまとめると、「\(n\) 番目のビットにゲートを置くと \(2^{n - 1}\) 離れた円同士が演算ペアとなる」というルールが導けることが分かると思います。 このルールを単純に覚えてしまってもよいですし、上記の理屈を理解しておくとさらに良いと思います。