グローヴァー探索
折り返し変換
位相を大きさに変換する
前節では、位相論理演算を使って計算結果を位相に出力する方法を見てきました。 たとえば充足可能性問題では、目指す論理式が true となるような変数の値 true/false の組合わせを探します。 これを位相論理演算で計算し、論理式を満たす振幅の位相を反転することで答が求まります。
しかし位相に埋め込んだ計算結果は簡単には取り出せません。 結果を取り出す唯一の手段は
折り返し変換は位相の差を確率の差に変換するアルゴリズムです折り返し変換の内容と動作については、折り返し変換の仕組みで説明します。。 論理位相演算によって反転した位相を折り返し変換にかけることで、位相反転でマークした振幅の確率を増幅させることができます。 この「位相反転→折り返し変換」を振幅増幅と呼び、量子探索であるグローヴァーのアルゴリズムの中心部分を担っています。
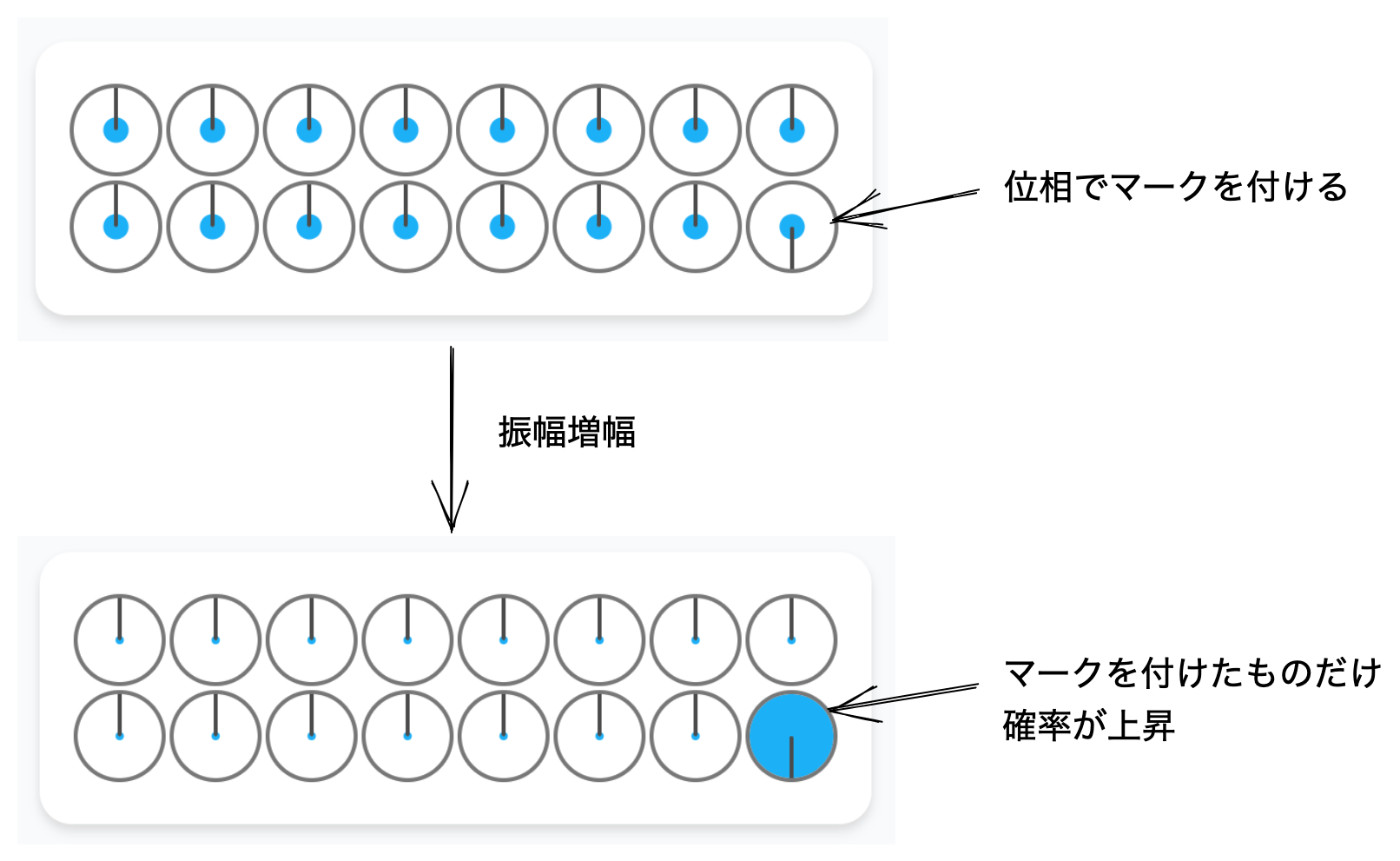
今回はこの繰り返し変換を見ていきましょう。
折り返し変換
まずは折り返し変換の実行例を見てみましょう。 例題として 2 量子ビットについて、上位ビット & 下位ビット = true
となる値を取り出すことを考えます。 2 量子ビットなので \(|00\rangle\), \(|01\rangle\), \(|10\rangle\), \(|11\rangle\) の 4 通りを考えると、このうち 上位ビット & 下位ビット = true となるのは \(|11\rangle\)
ひとつです。 つまり折り返し変換によって \(|11\rangle\) の確率が大きくなれば成功です。
これは次の 3 つのブロックを組合わせた回路として実装できます。
-
重ね合わせの準備
最初にそれぞれの量子ビットに
を適用し \(|00\rangle\), \(|01\rangle\), \(|10\rangle\), \(|11\rangle\) の確率をそれぞれ等しく 25% にします。 -
AND の結果を位相に書き込む
上位ビット & 下位ビット = trueは位相論理演算の AND (pAND) ひとつで簡単に実装できます。 -
折り返し変換
以下の折り返し変換を適用すると、位相が反転した振幅の確率を増幅し、ほかの確率を減衰させることができます。
以下の回路を実行すると、確かに答である \(|11\rangle\) の確率が 100% になり、それ以外は 0% になっていることがわかります。
より大きな量子ビット数での折り返し変換
折り返し変換の回路はほぼ形が決まっているので、量子ビットを増やしても同様に使えます。 たとえば 4 量子ビットの AND (答は \(|1111\rangle\)) でも、単純にゲートを増やすだけで構成できます。 以下の回路を実行すると \(|1111\rangle\) の確率が約 47.3 % に増幅され、その他の確率は約 3.5% まで減衰していることが分かります。
前回の充足可能性問題を解く回路にも適用してみましょう。 先ほどと同じく 4 量子ビットの折り返し変換の回路の末尾に追加するだけで、答の \(|00000000001000\rangle\) を確率的に浮かび上がらせることができます。
このように、折り返し変換の使いかたはとても簡単です。 重ね合わせ上で位相論理演算を実行する回路の最後に、折り返し変換を追加するだけで確率を増幅できます。
まとめ
位相に埋め込んだ計算結果を取り出すための、折り返し変換回路の使いかたを学びました。 位相論理演算と折り返し変換をまとめて振幅増幅と呼び、これによって確率を増幅させることで計算結果を読み出せるようにします。
次回は、振幅増幅を繰り返すことでさらに確率を増幅する方法を学びます。 確率を 100%
近くまで増幅することで、正しい答を
