複数量子ビットでの演算

複数量子ビットに対してゲートを適用するとどうなるでしょうか? 今までは単一の量子ビットに X ゲートや H ゲートを適用してきましたが、複数量子ビットに適用する場合でもそれぞれのゲートの働きは変わりません。 しかし、ゲートを配置したビット によって、演算の対象となる状態ベクトルの円が異なってきます。 ゲートを 1 ビット目、2 ビット目、3 ビット目、、、と順番に置いていくことによって、その動作を確認してみましょう。

ゲートを 1 ビット目に置いた場合

以降では 3 量子ビットの回路を例として考えます。この場合、状態ベクトルは \(2^3 = 8\) 個の円として表示されます。 この状態ベクトルに対して、X ゲートを 1 ビット目 (回路の一番上のワイヤ) に適用すると、X ゲートは「\(|0\rangle\) と \(|1\rangle\)」、「\(|2\rangle\) と \(|3\rangle\)」、「\(|4\rangle\) と \(|5\rangle\)」、「\(|6\rangle\) と \(|7\rangle\)」という隣同士の円 (1 つだけ離れた円同士) それぞれのペアに対して、X ゲートの動作である「円の入れ替え」を行います。

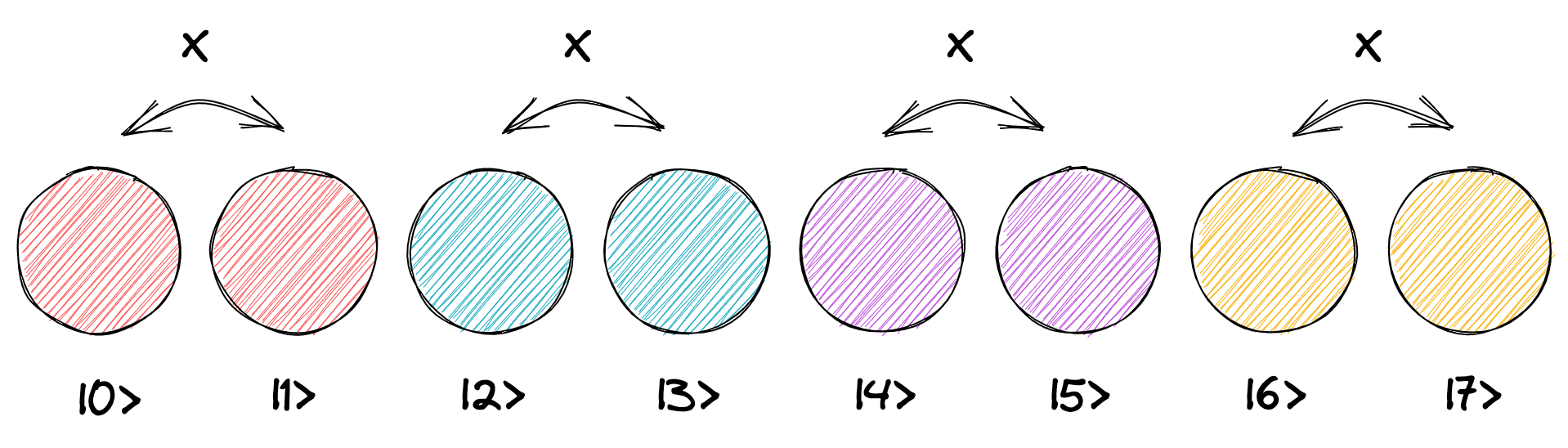
これを具体的な状態ベクトルで見ると、次のようになります。 \(|0\rangle\) と \(|1\rangle\)、\(|2\rangle\) と \(|3\rangle\)、… それぞれのペアの左右の円が、X ゲートによって入れ替わることが分かります。

この動作を Qni 上でも確認してみましょう。 下の回路で X ゲートの適用前と適用後を比べてみると、たしかに隣同士の円が X ゲートによって入れ替わっていることが分かります。

ゲートを 2 ビット目に置いた場合

ゲートを置く位置を変えると、ゲートが作用する円のペアが変化します。 先ほどと同じ状態ベクトルに対して、X ゲートを 2 ビット目に適用すると、X ゲートは「\(|0\rangle\) と \(|2\rangle\)」、「\(|1\rangle\) と \(|3\rangle\)」、「\(|4\rangle\) と \(|6\rangle\)」、「\(|5\rangle\) と \(|7\rangle\)」という 1 つ飛ばしの円同士 (2 つ離れた円同士) で作ったペアに対して、円の入れ替えを行います。

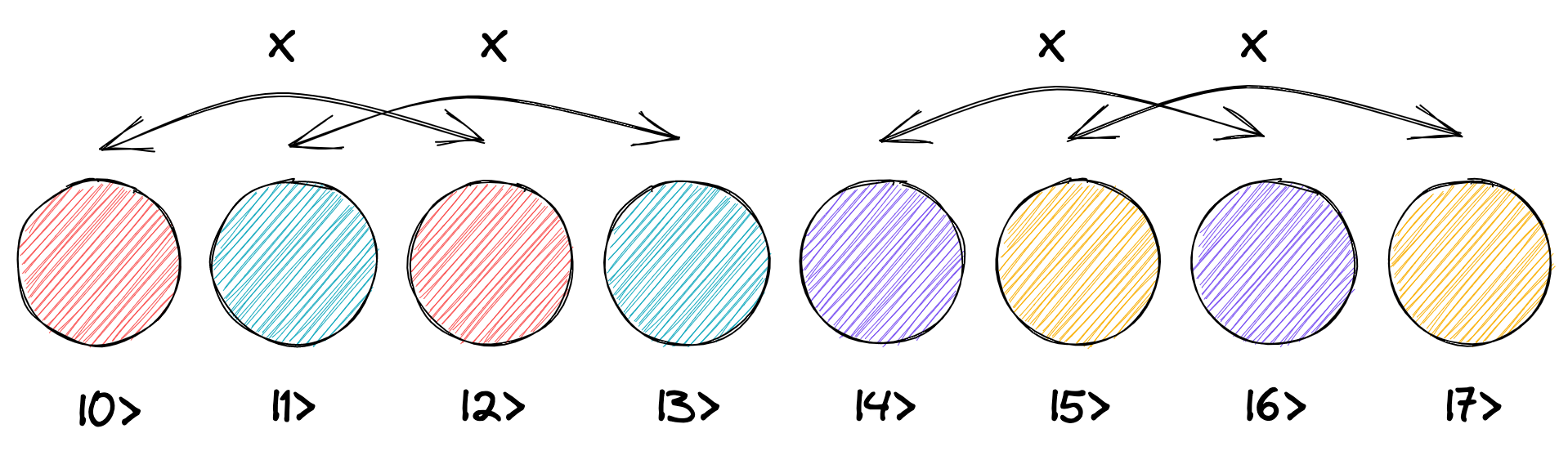
これを状態ベクトルで見ると、次のようになります。 \(|0\rangle\) と \(|2\rangle\) や \(|5\rangle\) と \(|7\rangle\) が X ゲートによって入れ替わることが分かります。

これも Qni で実際に確認しておきましょう。

ゲートを 3 ビット目に置いた場合

X ゲートを 3 ビット目に適用すると、4 つ離れた円同士で作ったペアに対して、円の入れ替えを行います。 つまり「\(|0\rangle\) と \(|4\rangle\)」、「\(|1\rangle\) と \(|5\rangle\)」、「\(|2\rangle\) と \(|6\rangle\)」、「\(|3\rangle\) と \(|7\rangle\)」のペアについて X ゲート演算が行われます。

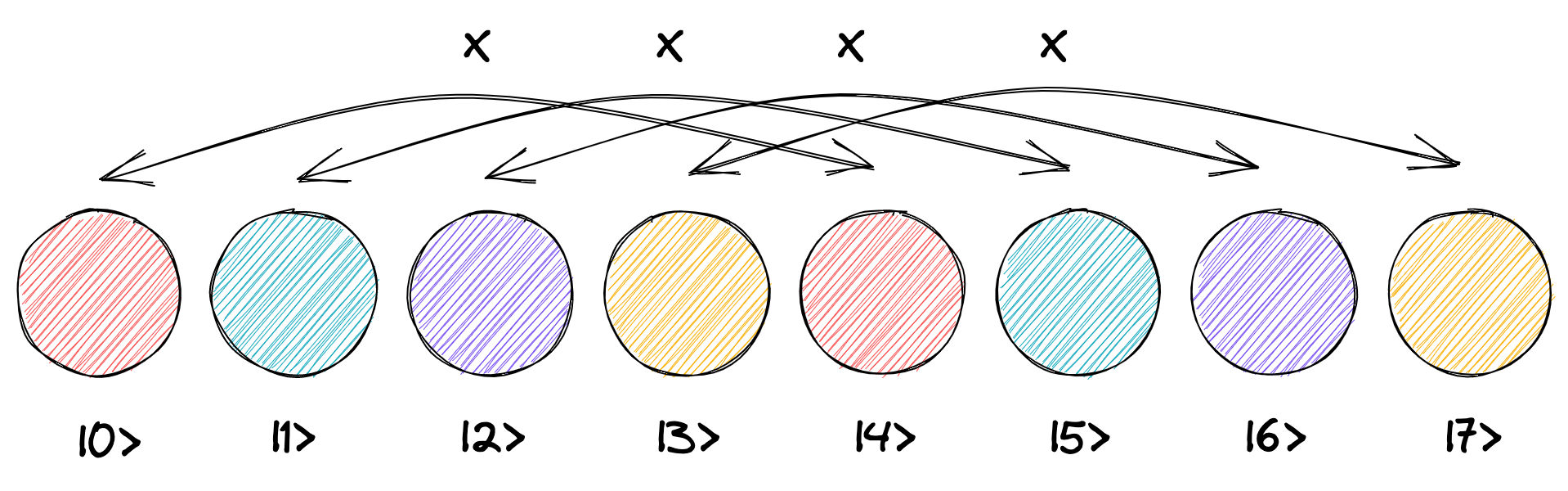
これはちょうど、円の前半 4 つと後半 4 つがそっくり入れ替わった形になります。

こちらも Qni で確認しておきましょう。

まとめ

複数の量子ビットにゲートを適用するには、次のように 2 段階に分けて考える必要があります。

• ゲートを置いたビット番号によって、ゲートを作用させるペア (演算ペア) を決める。
• それぞれの演算ペアについて、ゲートを適用する

演算ペアの決めかたは一般に、\(n\) 番目のビットにゲートを置くと \((n - 1)^2\) 離れた円同士がペアとなります。 たとえば 3 ビット目にゲートを置いた場合、\((3 - 1)^2 = 4\) なので 4 つ離れた円同士のペアを考えれば OK です。

なぜこのようになるかは、次項で詳しく説明します。