QPU は何が得意?

結局のところ、量子コンピュータ (QPU) は何が得意なのでしょうか。そしてさらに重要なことですが、メカニズム上の制限はあるのでしょうか。

いきなり結論

量子コンピュータが従来のコンピュータに勝てる計算は、行列の掛け算です。めちゃくちゃ大きい、指数関数的に巨大な行列を、同じように巨大なベクトルに対して、 たった 1 ステップで掛けることができます。

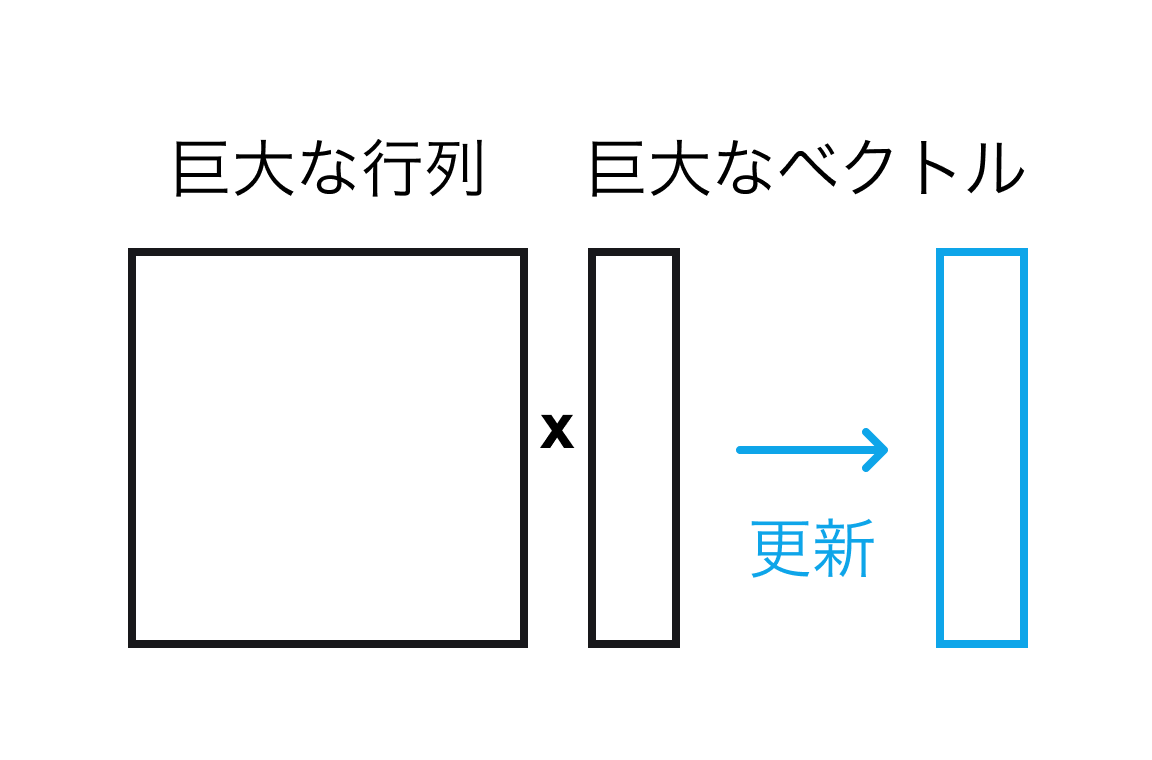
この行列とベクトルは、従来のコンピュータでは何に対応するでしょうか。 行列は、量子コンピュータが実行する命令にあたります。QPU 命令は数学的には巨大な行列として書き表すことができるためです。 ベクトルは量子ビットの内容を数として縦に並べたもので、ある時点での量子コンピュータの状態を表します。 つまり行列をベクトルに掛けるという操作は、QPU 命令を量子ビットに作用させることで、量子ビットの状態 (量子コンピュータの状態) を更新することにあたります。 つまり量子コンピュータは巨大な行列とベクトルの掛け算を高速に繰り返すことでその状態を更新し、これが量子コンピュータでのプログラム実行にあたります。

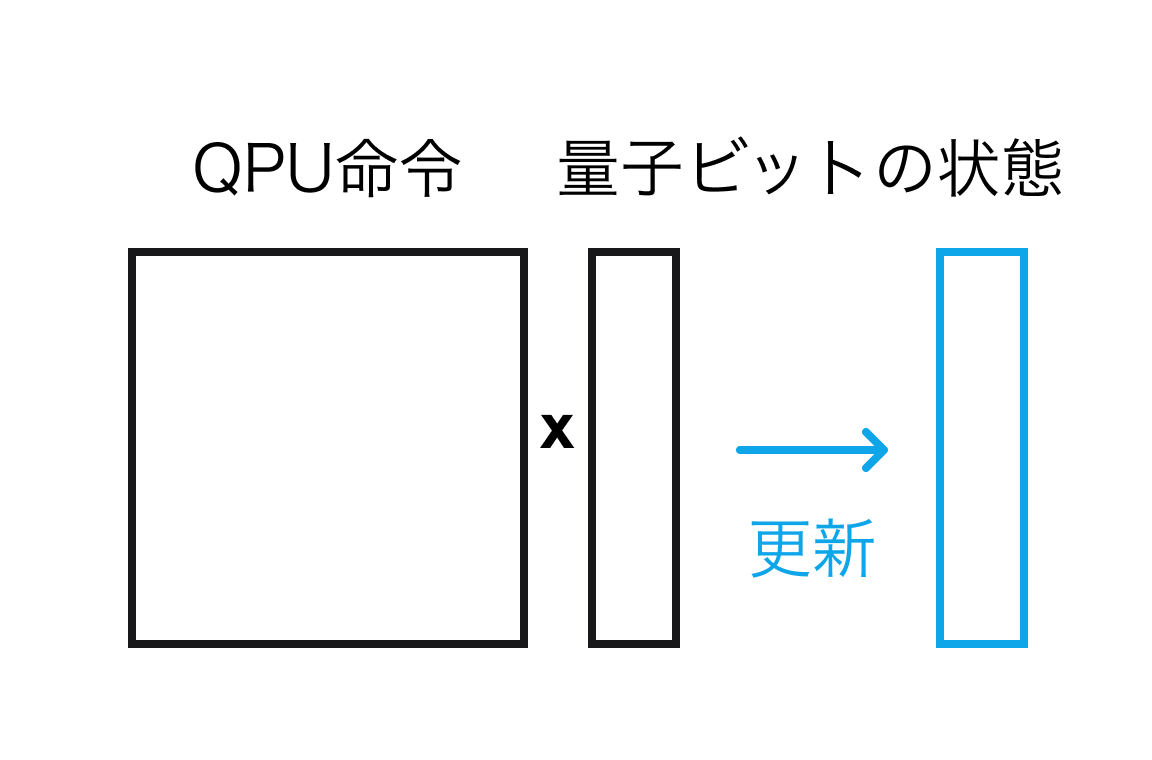
行列とベクトルの掛け算を知らなくても、行列計算がゲームの 3D CG やスパコンなどの数値計算などで活躍しているとなんとなく知っていれば、その重要さが分かるでしょう。 行列とベクトルの掛け算には大量の足し算と掛け算が含まれるので、それがたった 1 ステップでできるという量子コンピュータの能力は驚くべきものです。しかし落とし穴もあります。

• 巨大なベクトルを入力するのが大変なこと
• 使える行列に制限があること
• 計算結果が一筋縄では取り出せないこと

巨大なベクトルの入力

掛け算しようとするベクトルのデータは、当然ですが量子コンピュータに入力してやる必要があります。たとえば、3 量子ビット量子コンピュータで扱う情報の最小単位を量子ビットと呼びます。量子ビット数の大きい量子コンピュータほど規模の大きい計算ができます。現在最も量子ビット数が大きいマシンは 100 量子ビットを越える程度です。の量子コンピュータを持っている場合、入力するベクトルのデータは次のように数が 8 個ならんだものになります一般に、\(n\) 個の量子ビットを持つマシンでは、数を 2 の \(n\) 乗個ならべたベクトルの掛け算を実行します。

$$\begin{bmatrix} 0.5 \\ 0 \\ 0 \\ 0.707 \\ 0 \\ 0 \\ 0.5 \\ 0 \end{bmatrix}$$

ここでの問題は、値をセットしなければならないベクトルのサイズが \(2\) の \(n\) 乗とまさに指数関数であることです。 たとえば 100 量子ビットでは

$$2^{100} = 1267650600228229401496703205376$$

もの数をセットしなければならず、これには 1,000 年単位の膨大な時間がかかってしまいます。唯一の希望は、まっさらな初期状態のベクトルから始めて、量子コンピュータの中でいろんな行列を掛けていくことによって、計算的に入力データを作ることです。それでもほとんどの場合、合理的な時間では実行できません。

使える行列の制限

量子コンピュータが扱うベクトルは常に「二乗和が 1」という性質を保つ必要がありますベクトルの数をそれぞれ 2 乗して足し合わせると 1 になること。。 量子コンピュータに入力するベクトルと、行列とベクトルを掛けて新たにできるベクトルは、この性質を保たなければなりません。

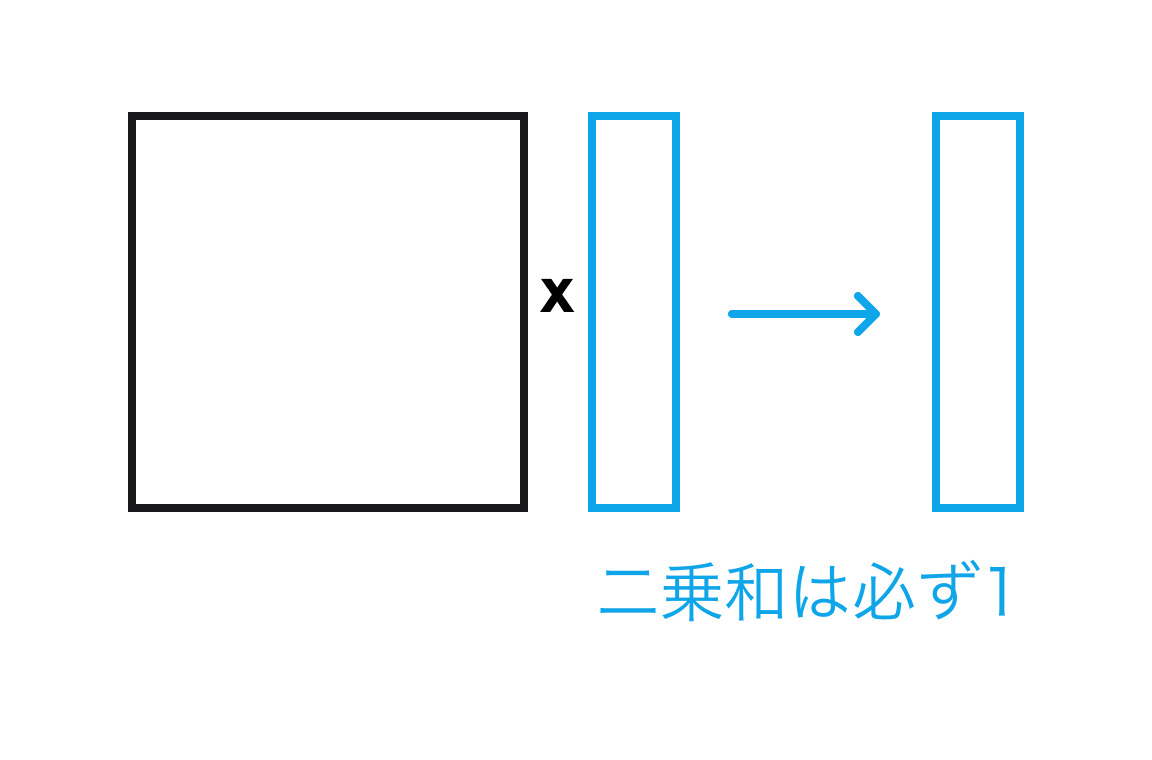
別の言い方をすれば、行列の掛け算はベクトルの二乗和を変えてはいけません。 この行列に対する制限は、量子力学に由来するものです。

制限その 2 として、行列の掛け算はいつも元に戻せる必要があります (行列の可逆性)。 つまり、ある行列 \(A\) を掛けたあとにやっぱり元のベクトルがほしくなった時、さらに行列 \(A^{\prime}\) を掛けてやることで元のベクトルが得られる必要があります行列の掛け算では、元に戻す行列 \(B\) が存在しないことがよくあります。。 こちらもやはり、量子力学に由来する制限です。

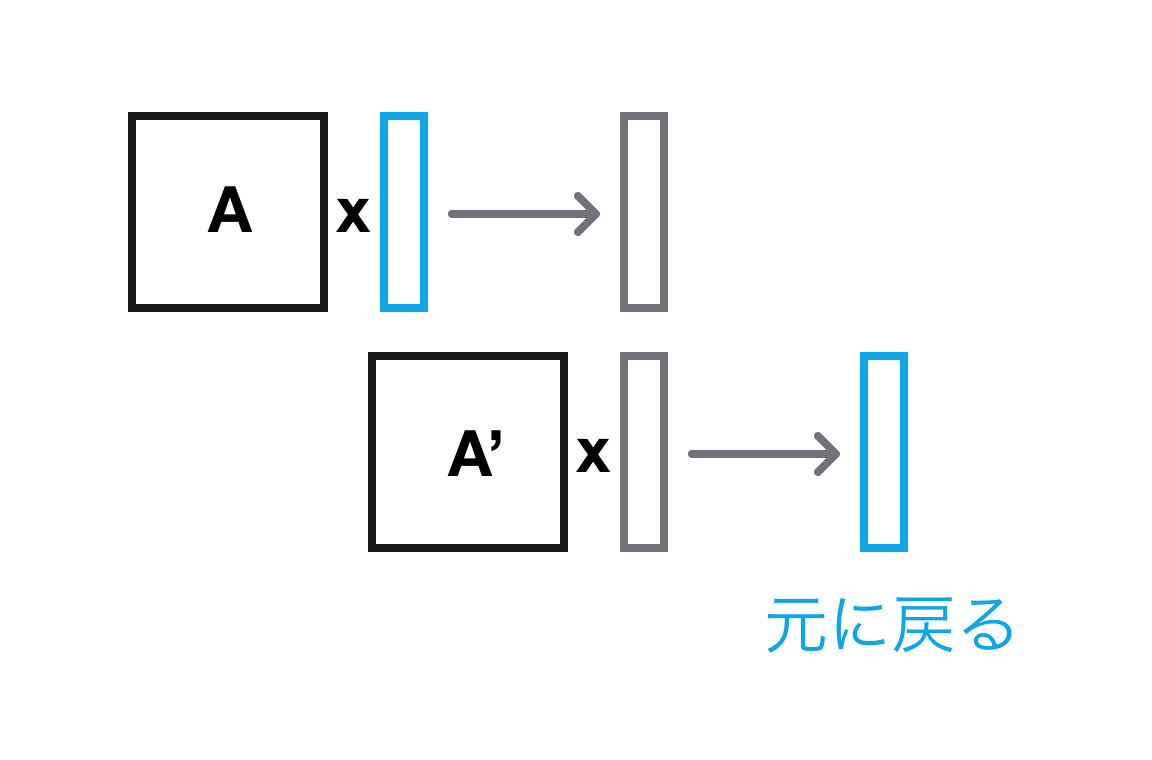
数学の用語では、これら 2 つの性質を満たす行列をユニタリ行列と呼びます。 なぜこの制限が難しいのか、著者が考えられる最も良い例えはルービックキューブです。 キューブをばらばらにして組み直すことで、直接的に色をそろえるのはルール違反です。 できるのは列を回転させることだけで、そこがチャレンジングな部分です。 量子コンピュータが扱うユニタリ行列も回転で構成されており、空間上の点や図形をある一定のルールで回転させる回転行列3D ゲームのキャラクター表示やカメラ移動には、回転行列がたくさん使われています。と呼ばれるものの一種です。

計算結果の取り出し

ここがおそらく一番トリッキーな部分です。 行列とベクトルの掛け算の結果のベクトルは、なんとそのまま取り出すことができません。 唯一できることは測定という操作で得られる別のベクトルを取り出すことだけです。

たとえば、量子コンピュータが掛け算の結果として次のベクトルを持っているとします。

$$\begin{bmatrix} 0 \\ 0.5 \\ 0 \\ 0 \\ 0.707 \\ 0 \\ 0.5 \\ 0 \end{bmatrix}$$

ここで測定を行うと、それぞれの成分が二乗され、確率 (\(\%\)) として解釈されます。

$$\begin{bmatrix} 0 \\ 0.5 \\ 0 \\ 0 \\ 0.707 \\ 0 \\ 0.5 \\ 0 \end{bmatrix} \longrightarrow \begin{bmatrix} 0^2 \\ (0.5)^2 \\ 0^2 \\ 0^2 \\ (0.707)^2 \\ 0^2 \\ (0.5)^2 \\ 0^2 \end{bmatrix} \longrightarrow \begin{bmatrix} 0\% \\ 25\% \\ 0\% \\ 0\% \\ 50\% \\ 0\% \\ 25\% \\ 0\% \end{bmatrix}$$

そしてそれぞれの確率に従って、その成分だけを 1 とするベクトルが出力されます。 ユーザはこれらのベクトルのうちどれか 1 つだけを、確率的に取り出すことしかできません。

$$ \begin{bmatrix} 0\% \\ \textcolor{red}{25\%} \\ 0\% \\ 0\% \\ \textcolor{red}{50\%} \\ 0\% \\ \textcolor{red}{25\%} \\ 0\% \end{bmatrix} \longrightarrow \begin{bmatrix} 0 \\ \textcolor{red}{1} \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \end{bmatrix}\ または\ \begin{bmatrix} 0 \\ 0 \\ 0 \\ 0 \\ \textcolor{red}{1} \\ 0 \\ 0 \\ 0 \end{bmatrix} または\ \begin{bmatrix} 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ \textcolor{red}{1} \\ 0 \end{bmatrix} $$

これは結局、何を意味するでしょうか? 量子コンピュータでの行列とベクトルの掛け算は、出力するベクトルを決める確率の素もと (二乗すると確率になる数) を計算しているのです量子コンピュータが扱うベクトルの二乗和が 1 というルールは、確率から来ています。つまり、測定によって出てくるベクトルそれぞれの確率をすべて足すと 100% にならなければならないため、二乗和は必ず 1 となります。。 測定した瞬間に元のベクトルは破壊され、最終的には 1 つの成分だけが 1 でほかはすべて 0 となるベクトルだけが確率的に取り出せます。 どう考えても奇妙な動作ですが、これも量子力学のルールに従ったものです。

まとめ

量子コンピュータは巨大な行列とベクトルの掛け算を高速に行えます。しかし、入力データであるベクトルは巨大なため、計算的に作ることしかできません。 また、ベクトルに掛けることのできる行列は回転をあらわす特別な行列のみです。 そして、掛け算の結果を直接取り出すことはできず、必ず測定を通して単純なベクトルしか取り出せません。

こんなに厳しい制約が課せられた上でも、うまく動作する量子アルゴリズムがいろいろと提案されています。 たとえば後に見る量子フーリエ変換 (QFT) アルゴリズムは、量子因数分解などの中間的なステップとして動作することで、測定することなく計算結果をそのまま次のステップへと渡します。