ランダムバイトジェネレータ

量子乱数ジェネレータMEASUREMENT 命令を参照は 1 ビットの乱数 0 または 1 を生成するものでした。 より大きな乱数を生成するにはどうしたらよいでしょうか? 今回は 8 個の量子ビットを使って、1 バイト (= 8 ビット, 0 から 255 まで) の乱数を生成する回路を紹介します。

次の回路は、1 ビット目から 8 ビット目それぞれに H ゲートを適用し、最後にすべてのビットを測定します。 測定すると 0 から 255 までの数のうちどれか 1 つをランダムに出力します。

大筋としてこれがどのように動作しているか、状態ベクトル表示を使って調べてみましょう。 H ゲートを全ビットに適用した時点の状態ベクトルを見ると、\(|0\rangle\) から \(|255\rangle\) それぞれの確率は等しく 0.390625% (100 / 256 %) になります。 これを測定することで、\(|0\rangle\) から \(|255\rangle\) のうちどれか 1 つがランダムに出力されます。

等しい重ね合わせができる仕組み

なぜ等しい重ね合わせ状態ができるか、H ゲートを 1 つずつ適用した時の状態ベクトルを詳しく見てみましょう。 以下では、スペースの都合上 3 量子ビットまでを見て行きます。

初期状態で 1 ビット目に H ゲートを適用すると、複数量子ビットにゲートを適用したときのルール複数量子ビットでの演算を参照より、隣同士の円それぞれのペア に対して H ゲートが適用されます。

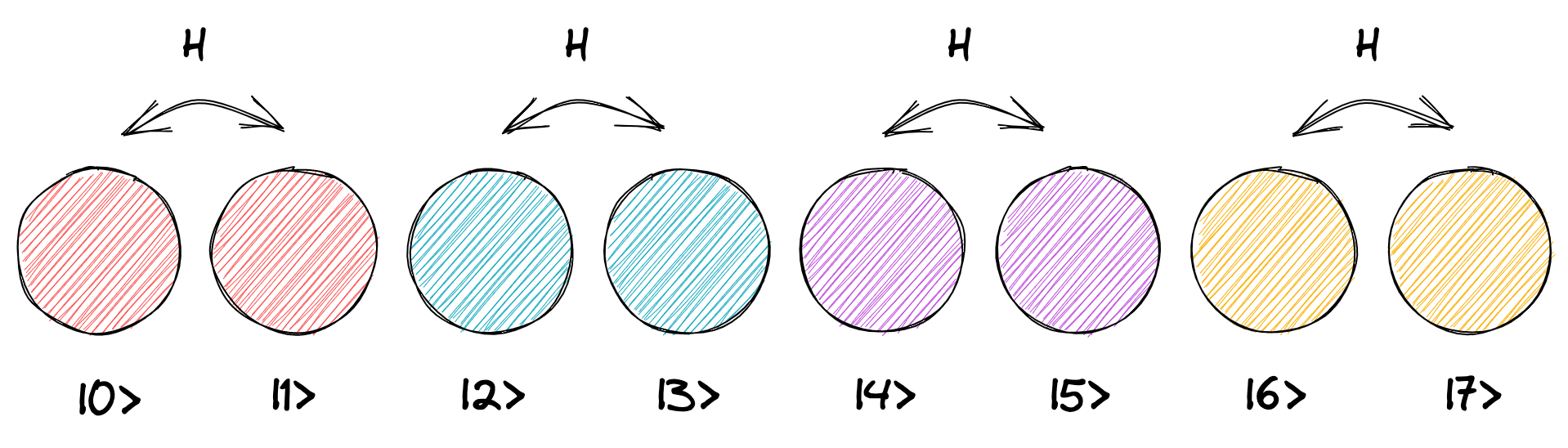
H ゲートはシンプルな重ね合わせを作る命令で、\(|0\rangle\) の確率を等しく \(|0\rangle\) と \(|1\rangle\) に割り振りますH ゲート参照。 ここでは 4 つのペアのうち、最初のペアの左側の円だけが確率 100% を持っています。 そこで最初のペアだけが 50% の重ね合わせ状態となり、ほかのペアは変化しません。

ここで 2 ビット目に H ゲートを適用すると、2 つ離れた円同士のペアそれぞれに H ゲートが適用されます。

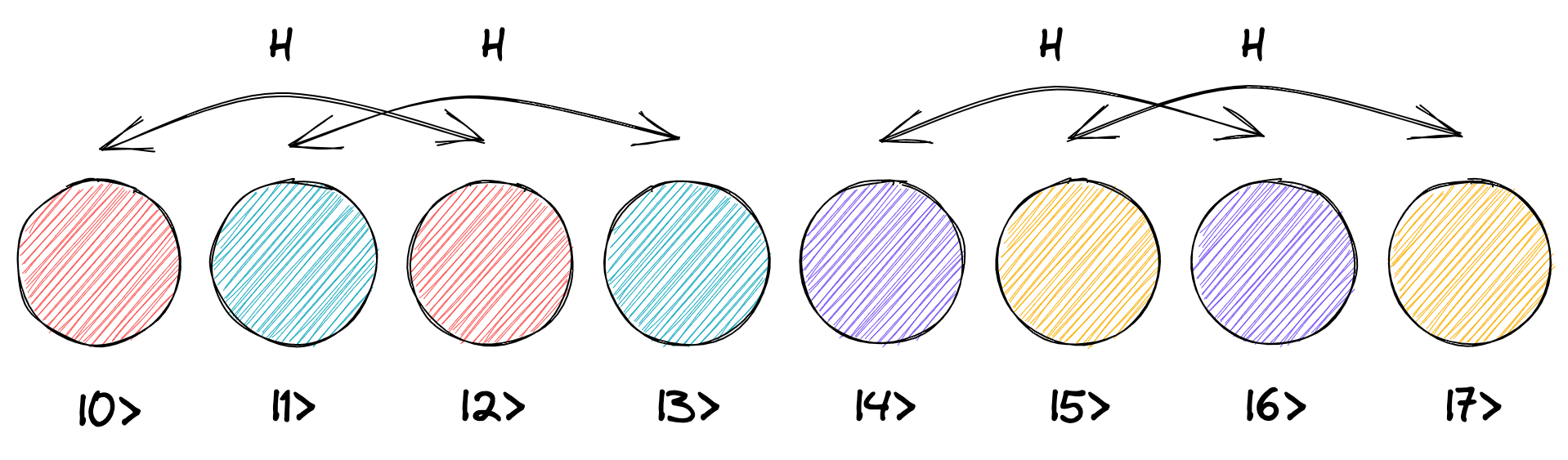
ここでは 4 つのペアのうち、「\(|0\rangle\) と \(|2\rangle\)」、「\(|1\rangle\) と \(|3\rangle\)」のペアの左側の円が確率 50% を持っています。 そこでこれらのペアだけが 25% の重ね合わせ状態となり、ほかのペアは変化しません。

同様に 3 ビット目に H ゲートを適用すると、4 つ離れた円同士のペアについて、全ペアの左の円が確率 25% を持っているので、すべての円が等しく 12.5% の重ね合わせ状態となります。

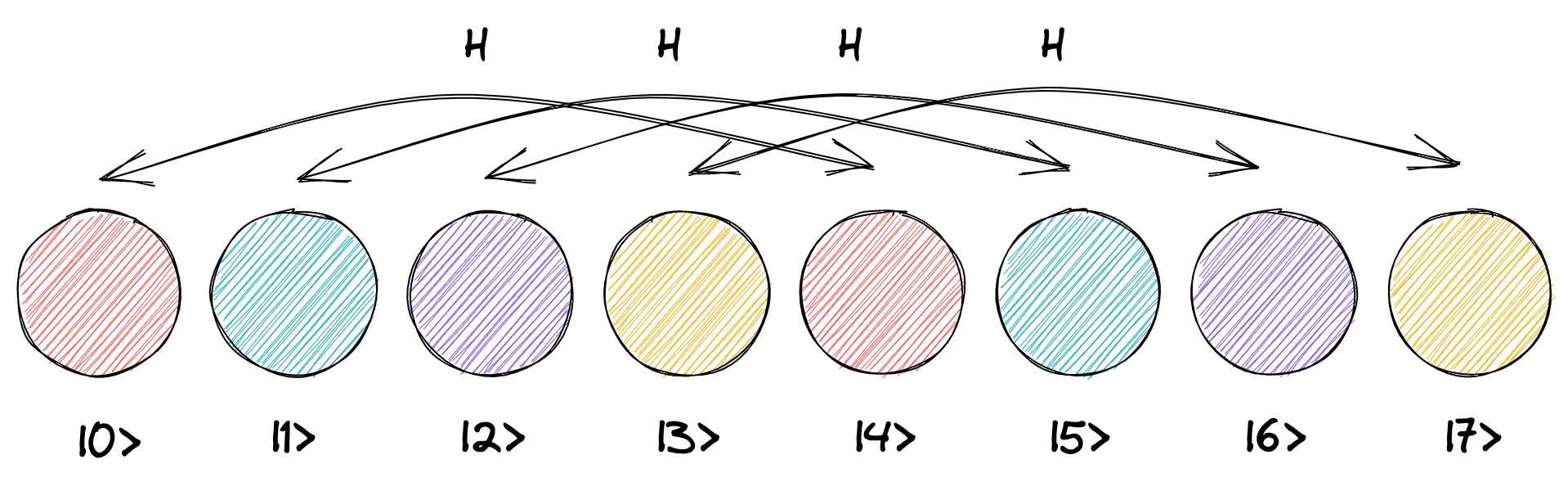
同じプロセスを 4 ビット目、5 ビット目、… と続けていくことで、最終的にすべての円が等しく確率 0.390625% (100/256 %) を持つようになります。

回路をコンパクトにする

最初の回路で 1 ビット目から 8 ビット目まで置いた H ゲートは、それぞれが置かれたビットのみに作用します。 つまり、異なるビットに置いた H ゲートはそれぞれ他のゲートとは独立して実行されるので、可能な限り左に詰めることで他のゲートと同時に実行できます。 このことを使うと、先ほどの回路は次のようにかなりコンパクトに書き直せます。

多くの量子アルゴリズムでは、最初の準備段階として、均一な重ね合わせ状態をこのように縦に並べた H ゲートで作ります。 非常によく使うパターンですので覚えておきましょう。