H ゲート

H ゲート はフランスの数学者、ジャック・サロモン・アダマール (Jacques Salomon Hadamard, 1865 - 1963) の名前を冠したゲートで、別名アダマールゲートとも呼びます英語では「ハダマードゲート (Hadamard gate)」と言います。日本語の「アダマールゲート」は、フランス語の元々の発音 (Hadamard の最初の h と最後の d を発音しない) に近いカタカナ表記です。。

はシンプルな重ね合わせ状態を作ります。 \(|0\rangle\) または \(|1\rangle\) に作用させると、次のように大きさの等しい重ねあわせ状態を作ります。

\(|1\rangle\) に対して を適用したときのみ、\(|1\rangle\) の位相が π 変化していることに注意してください。 \(|0\rangle\) に対する 操作は、位相の回転を含みません。

は QPU 独自の命令です。量子ビットだけが持つ重ね合わせ状態を作るという性質を持つので、従来の論理演算には H ゲートに対応するものはありません。

ハンズオン

を \(|0\rangle\) と \(|1\rangle\) に適用して、重ね合わせ状態が作られることを確認しましょう。 \(|0\rangle\) は最初から回路にセットされていますが、\(|1\rangle\) を作るにはどうしたらいいでしょうか? (ヒント: X ゲートを使います)

逆演算

を続けて 2 回適用するとどうなるでしょうか? 直感的には分かりづらいですが、そんな時には Qni で試してみましょう! 実際に を 2 個連続して置くと、\(|0\rangle\) も \(|1\rangle\) もそれぞれ元の状態に戻ります。 つまり、 も X ゲートと同様にそれ自身を打ち消す効果を持っているので、それ自身の逆演算です。

H ゲートを回転として見る

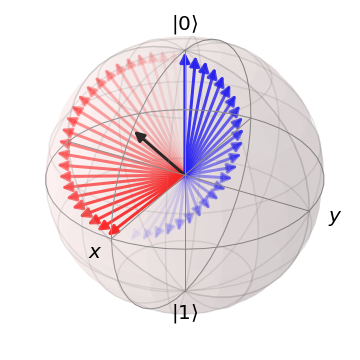
を回転として見ると、 はブロッホ球の X 軸と Z 軸の中間 (黒い矢印) を軸とした 180 度の回転となります。 たとえば北極の \(|0\rangle\) 状態に を適用すると、赤い矢印に沿って X の文字の部分まで回転します。 もう一度適用すると、青い矢印に沿って 180 度回転し元の位置に戻ります (逆演算)。

H ゲートの回転 (画像クレジット: physics.stackexchange.com)

任意の重ね合わせ状態に H ゲートを適用

次のように振幅の大きさと位相の異なる重ね合わせ状態に H ゲートを適用した場合、その変化はどのように理解するとよいでしょうか?

これを頭の中だけで想像するのは大変なので、さしあたっては Qni に計算をおまかせして OK です。 実は、円の図だけでおおまかな変化を導き出すこともできるのですが、そのためには H ゲートを行列で表したもの (ゲートの行列表現) の知識が必要になります。 詳しい方法はのちほど紹介します。