量子ビット

量子ビットは、確率的ビットと非常によく似ています。主な違いは 2 つだけです。

• 確率のかわりに振幅 (amplitude) という値を使って状態を表現します。 確率は正の値を持ちますが、振幅は負の値も持ちます。
• 振幅は測定中に 2 乗され確率となりますQPU は何が得意? で紹介した測定で、確率を求めるために 2 乗の計算をしたことを思い出してください。。 つまり「振幅の 2 乗 = 確率」です。

Qni の円表示では、振幅は確率を表す青い円の半径を表します。 円の面積は半径の 2 乗 x π、つまり振幅の 2 乗かける π なので、青い円の面積は確率に正比例します。

確率

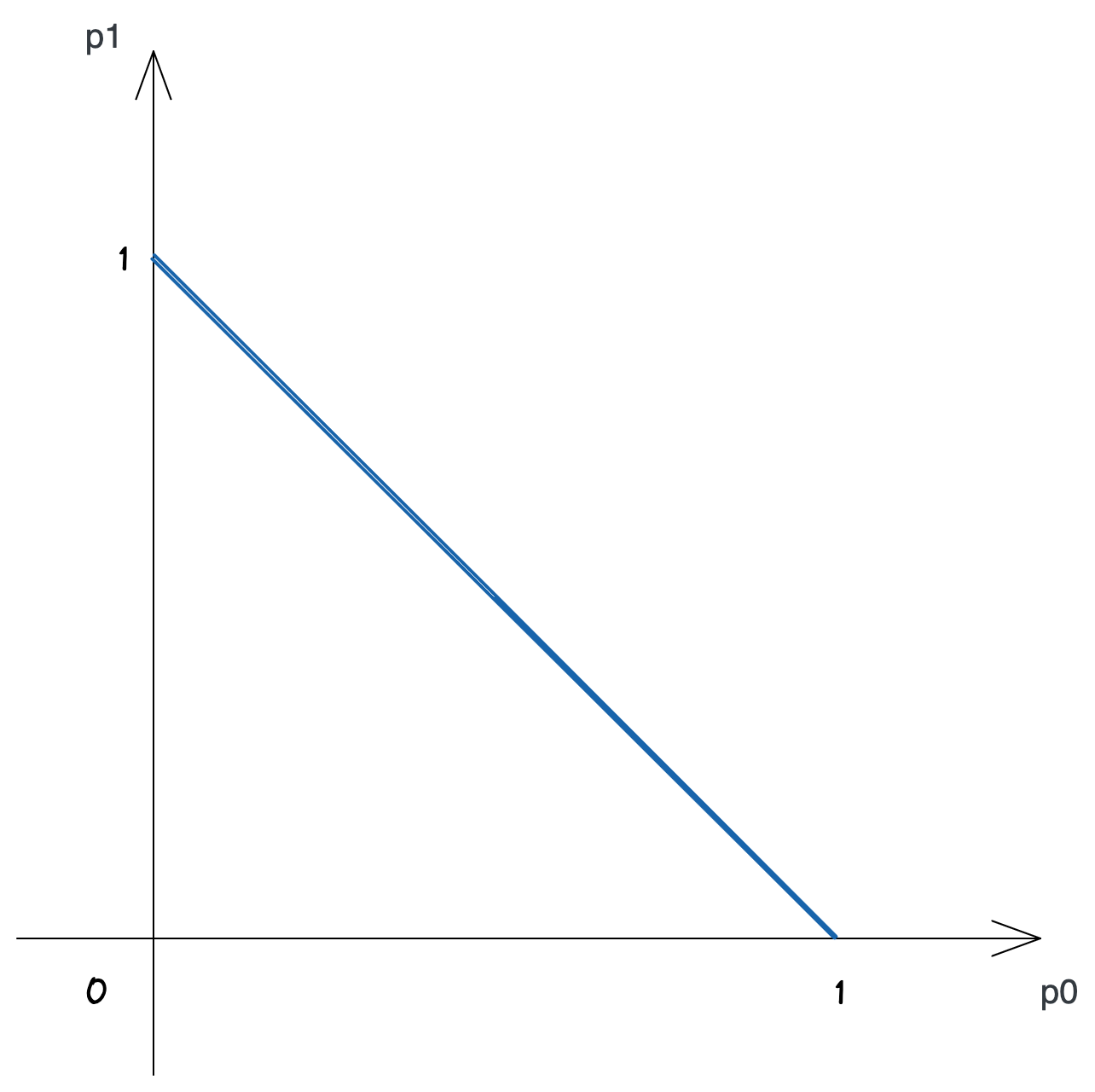
最初に、確率的ビットが取り得る状態をおさらいしてみましょう (コイントスの例を使ったことを思い出してください)。 ビットが 0 の状態をコインの表、ビットが 1 の状態をコインの裏とし、それぞれの確率を \(p_0,\ p_1\) とします。 表と裏の確率を足すと必ず 1 になり、またそれぞれの確率は 0 から 1 の間ですから、

$$p_0 + p_1 = 1\qquad (0 \leq p_0 \leq 1,\ 0 \leq p_1 \leq 1)$$

が成り立ち、確率的ビットが取りうるすべての状態を表す次のグラフが得られるのでした。

振幅

次は振幅を持つ量子ビットの取り得る状態をグラフにしてみましょう。 振幅は 2 乗すると確率になるのですから、ビットが \(|0\rangle\) となる確率の振幅を \(a_0\)、ビットが \(|1\rangle\) となる確率の振幅を \(a_1\) とすると、\(a_0^2 = p_0,\ a_1^2 = p_1\) が成り立ちます。 これを先ほどの式に入れると、

\begin{split} &p_0 + p_1 = 1 \\ \\ \Longrightarrow\ &a_0^2 + a_1^2 = 1\qquad (-1 \leq a_0 \leq 1,\ -1 \leq a_1 \leq 1) \end{split}

となり、このグラフは半径 1 の円になります。つまり、量子ビットの状態はこの円のうちの 1 点となります。

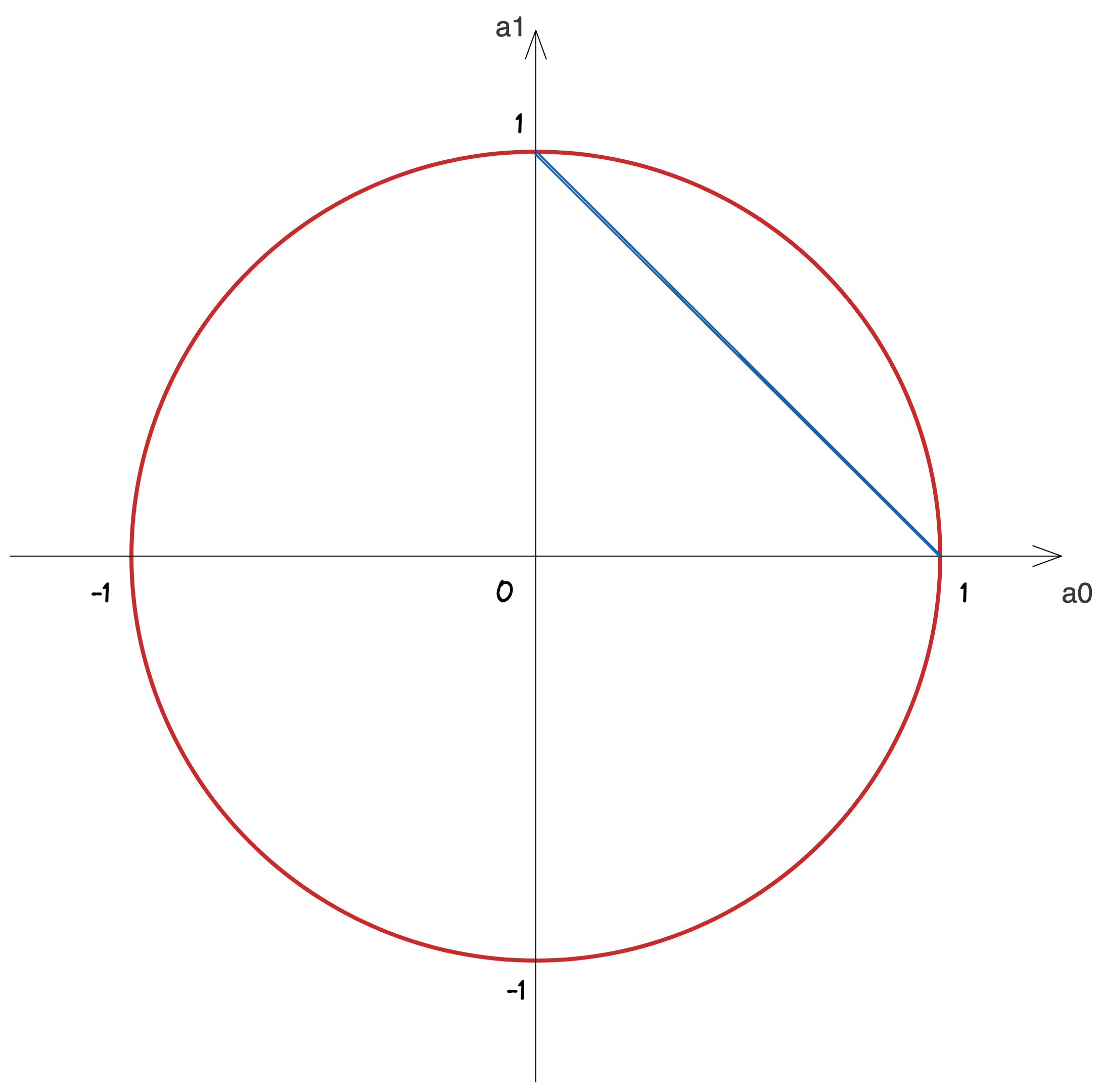
これを見て分かる通り、量子ビットが確率的ビットに比べて決定的に違うのは、振幅は負の値を持ち得ることです。 ここでは「量子ビットは確率的ビットよりもさらに広い範囲の情報を表現できそうだ」ということを視覚的に理解してもらえれば十分です。

振幅は複素数

実は、振幅は一般には複素数の値を取ります。 ここでは複素数の詳しい説明や計算は省きますが、この場合に量子ビットが取りうる状態を図にすると半径 1 の球表面になります。 これをブロッホ球ブロッホ球の名前はスイス出身の物理学者、フェリックス・ブロッホに由来します。と呼びます。

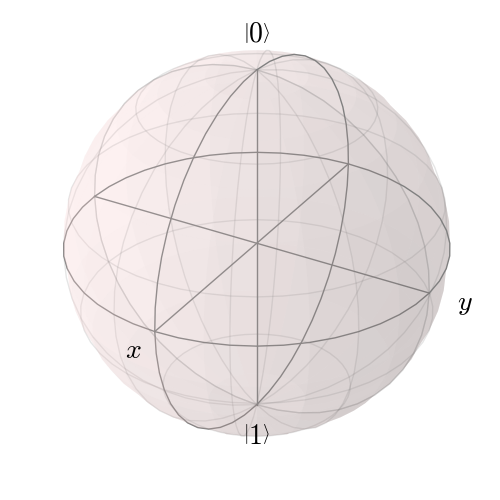
これをひらたく言えば、1 量子ビットの状態は地球上のとある 1 点として表せることになります (東京とか、ニューヨークとか、南極とかあなたの好きな場所をどこでも思い浮かべて OK です)。 この場合、状態 \(|0\rangle\) は北極点、状態 \(|1\rangle\) は南極点にそれぞれ対応します。

量子コンピュータが唯一得意な計算は、回転をあらわす行列をベクトルに掛けることでしたQPU は何が得意? を参照。。 これを地球で考えると、地球上のある点を回転操作で別の位置に移動させることに相当します。 これはたとえば、南極点 \(|1\rangle\) にいるペンギンの位置をベクトルとして表したとき、そのベクトルに球面上の回転を表す行列をかけることで、ペンギンを北極やハワイなど好きな場所に移動させることに相当します。

ブロッホ球で実験

Qni にはちょうど、1 量子ビットの状態を球上の点として表示する「ブロッホ球」命令があります。 これを使って、量子ビットのいろんな状態を見てみましょう。

下の量子回路には、すでにいくつかの QPU 命令が置いてあります。 それぞれの QPU 命令は、量子ビットに対する異なる回転操作を表しています。 ブロッホ球を回路上のいろんな場所に置いてみることで、それぞれの命令によってどんな回転が起こるか推測してみましょう。