位相論理演算の組合わせ

位相論理演算を組合せて、より複雑な論理式回路を作ってみましょう。 重ね合わせ上での論理演算 で見た a OR (NOT b) AND c の位相版はどうなるでしょうか？

位相論理演算を組合わせる場合、単純に pOR や pNOT を並べるだけでは動作しません。 なぜならば、位相論理演算は入力としての振幅を取るものの、出力は位相に書き込むからです。 このため、ただ並べただけでは入力と出力が合わずうまく連結できません。

位相論理演算を連結するには、普通の論理演算と位相論理演算を組合わせる必要があります。 a OR (NOT b) AND c を例にとると、最初の 2 つの論理演算 (NOT b とその結果を使ったa OR (NOT b)) は普通の論理演算 NOT, OR を連結して回路を作り、 最後の ... AND c の部分だけ位相論理演算 pAND にします。 このように最後の論理演算だけ位相論理演算にすることで入力と出力がマッチし、結果を位相に書き込むことができます。

この回路の実行結果は以下のようになります。振幅の大きさは最初の均等な重ね合わせ状態から変化せず、答の 4, 5, 7 のみ位相が反転していることが分かります。

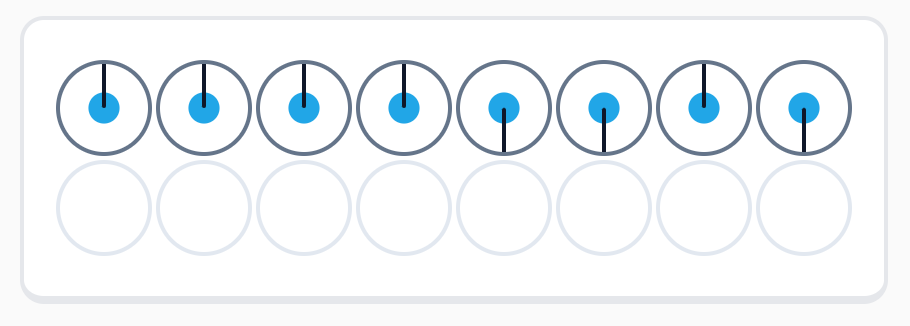
重ね合わせ上での論理演算で見た、論理演算回路の結果と比べてみましょう。 こちらは重ね合わせになっている振幅のうち、答の振幅とそうでない振幅の区別がつきません。 このため、読み出す確率が均等となり、答を読み出すのにたくさんの測定が必要になるのでした。

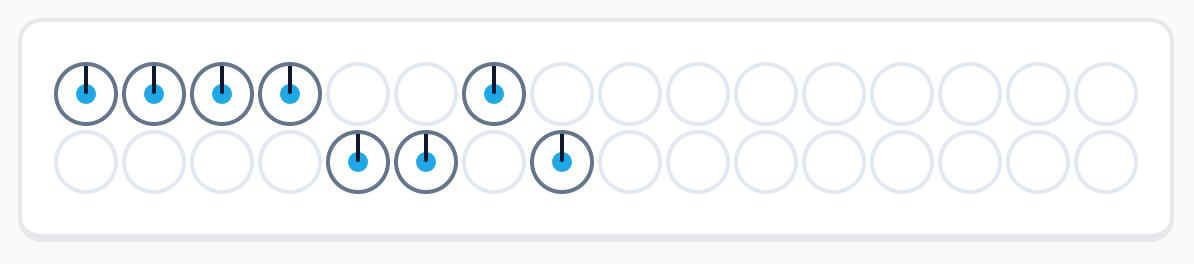
位相論理版の実行結果も振幅の大きさでは区別がつかないものの、位相ではっきりと区別がつきます。 繰り返しになりますが、これを後で紹介する振幅増幅プロセスにかけることによって、振幅の大きさへと反映でき、答をうまく読み出すことができるようになります。