\(a^xmod(N)\) の実装

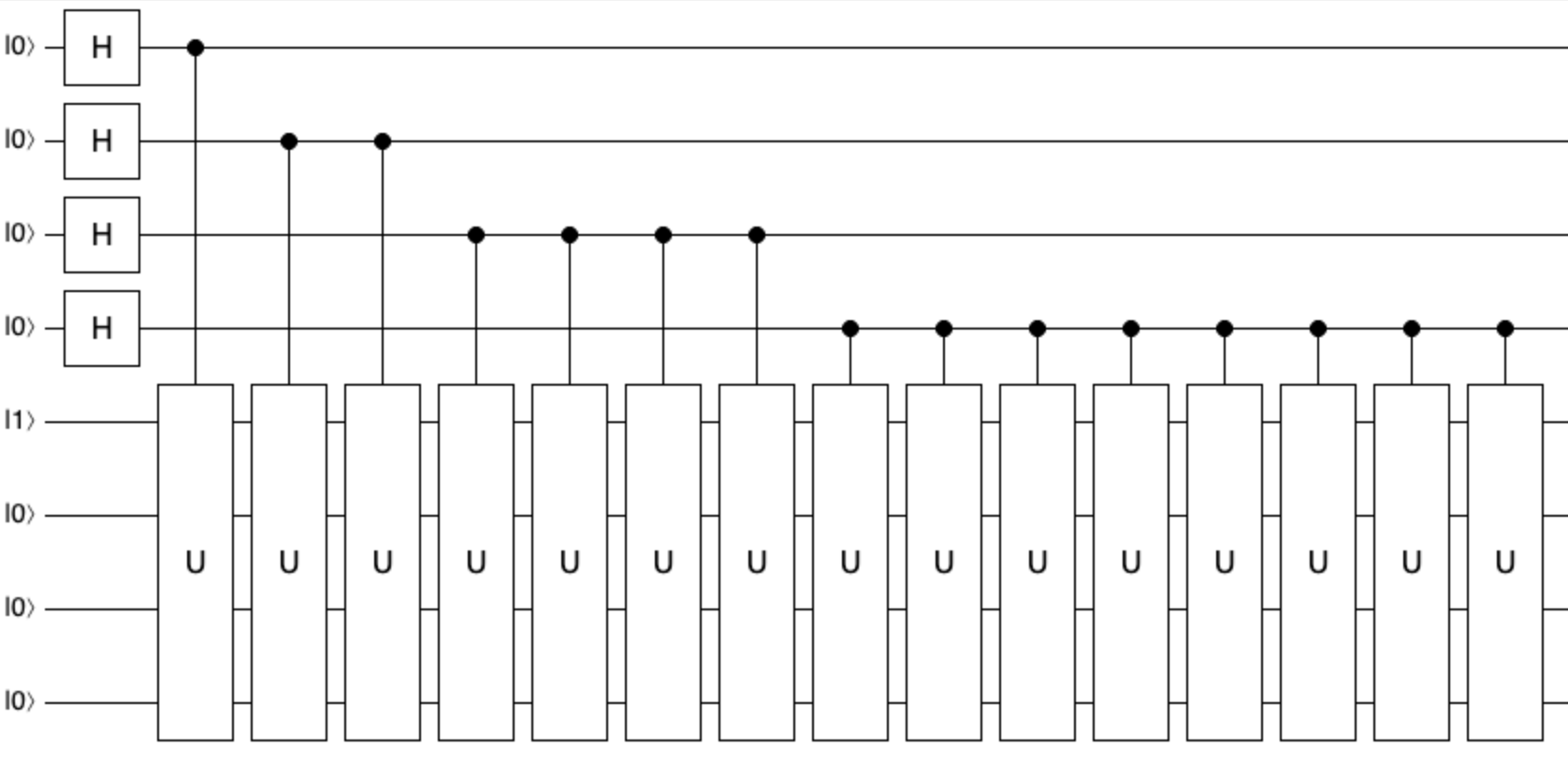
今回はいよいよ、\(a^x\,mod(N)\) を実際に計算できる回路を実装します。 前々回では、ブラックボックスである U ゲートをいくつも使った場合の実装を見てきました。 この実装では、U ゲートの一つひとつは \(a\,mod(N)\) を計算するのでした。 今回は、これらの連続した U と同じ動作をする一つの \(a^xmod(N)\) 回路 (べき剰余回路) の実装を考えます。

まともに実装した場合

べき剰余回路は、まともに実装すると非常に大きくなります。 V. Vedral らの論文V. Vedral, A. Barenco, A. Ekert, Quantum Networks for Elementary Arithmetic Operations (2021) には、べき剰余回路の実装方法が詳しく載っています。

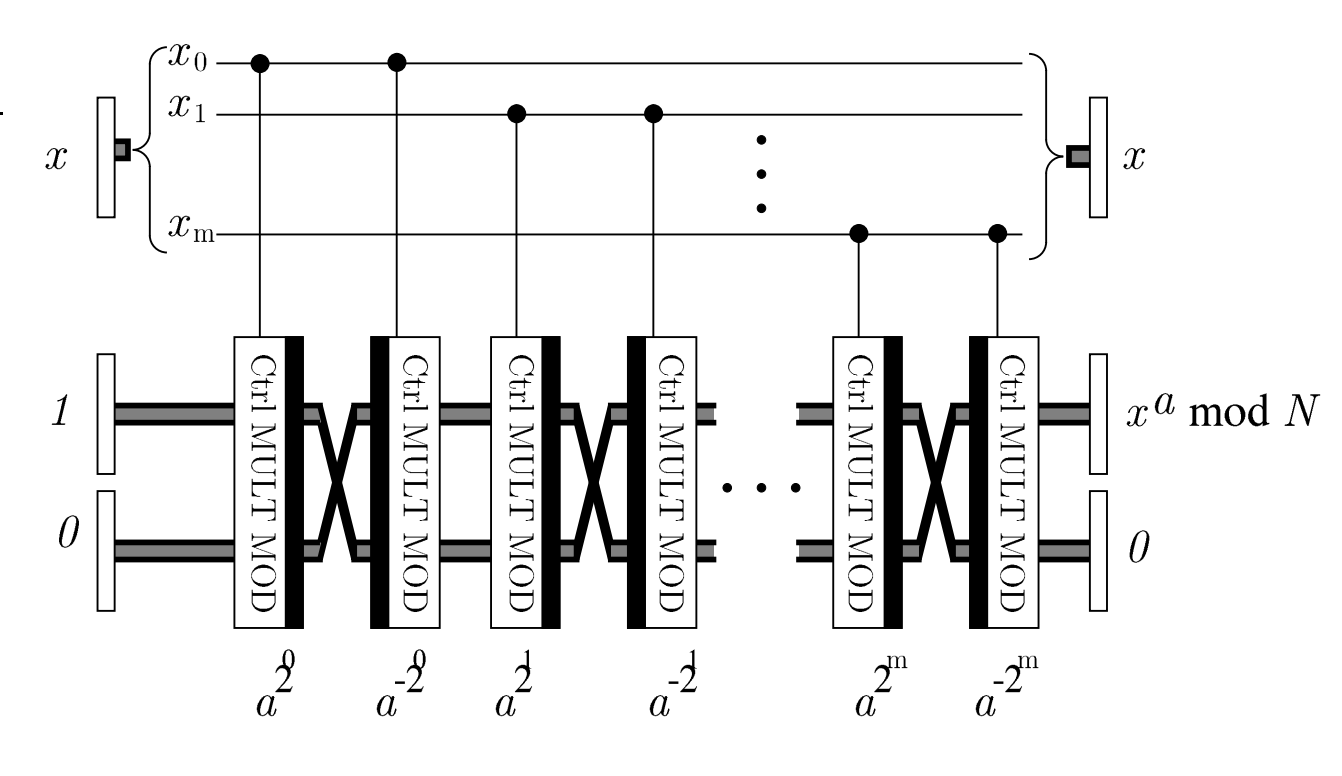
べき剰余回路の大まかな構成は、Ctrl MULT MOD という部品と をいくつか並べた形になります。 Ctrl MULT MOD は制御つき剰余乗算のことで、(その意味は置いておいて) 次のような回路になります。

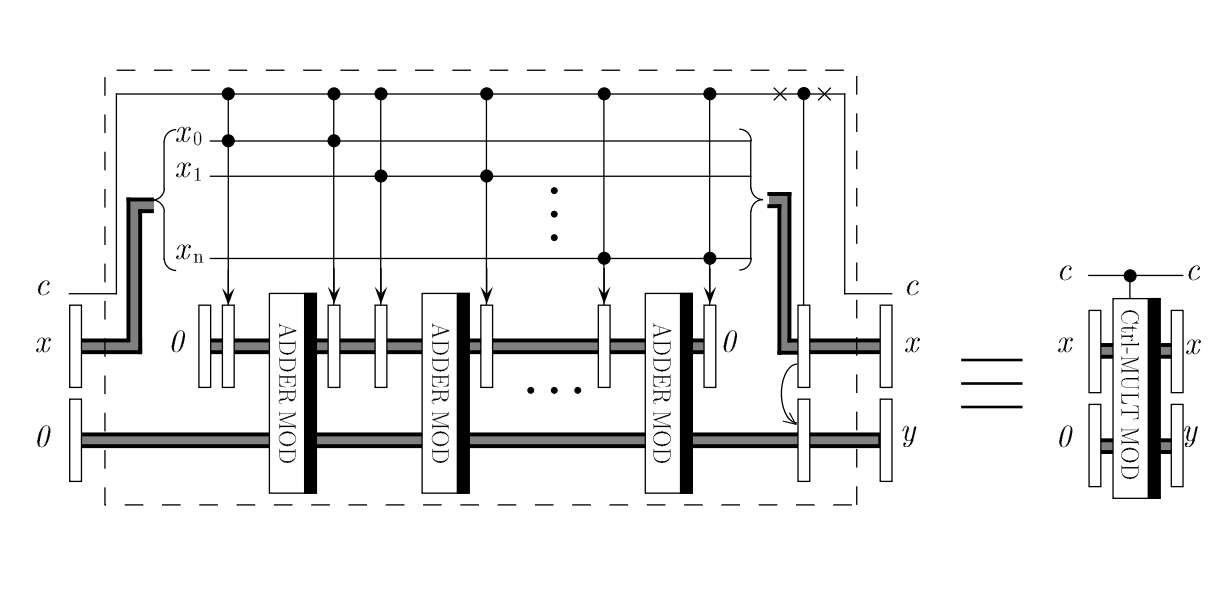
見ると Ctrl MULT MOD の中にも ADDER MOD と呼ばれる別の部品が入っており、こちらもゲートを組合わせて実装する必要があります。 このように、べき剰余回路はさまざまな部品を階層的に組合わせることで構成できる大規模で複雑な回路です。

これをそのまま Qni で実装すると Qni の最大量子ビット数 16 を簡単に超えてしまうため、今回は別の方法を採ります。

べき剰余回路の小さい (ずるい) 実装

今回はべき剰余回路のずっと小さい実装を見てみましょう。 \(a\) と \(N\) を固定し、かつあらかじめ \(r\) が分かっている場合であれば (= 因数分解の答があらかじめ分かっているならば)、べき剰余回路はとても短く実装できます。 答を利用しているのでちょっとずるいのですが、実行結果は本来のべき剰余回路と変わらないので、ショアのアルゴリズムの動作を見るぶんには問題ありません。

まずべき乗 \(a^x\) の部分について、今回は \(a = 2\) を選択します。その理由は、\(2^x\) は論理演算ではシフト演算で簡単に実装できるからです。 \(2^x\) を計算するには左シフトを \(x\) 回、つまり x ビットほど上位ビットへずらすだけです。このビットをずらすという操作は で実現できます。ビットのずらしを によるビットの入れ替えとして書くことで、量子回路でのシフト演算が実現できます。

また剰余 \(mod(N)\) については、シフト演算のラップアラウンドで実現できます。 ラップアラウンドとは、左シフトしたときに最上位ビットを最下位ビットにぐるっと回して移動する操作です。 たとえば 4 ビットであれば、1000 を左シフトすると 0001 となります。 \(mod(15)\) の場合、10 進数の 8 (二進数で 1000) を左シフトすると 16 になりますが、4 ビットのラップアラウンドを考えると 0001 になります。 \(16\,mod(15) = 1\) なので、確かに剰余が正しく求まっています。

べき剰余回路

シフト演算とラップアラウンドで \(2^x mod(15)\) を計算する回路を見てみましょう 説明の都合上、\(2^x mod(15)\) を書き込む用の 4 量子ビットと \(x\) を入れる用の 4 量子ビットを上下入れ替えてあります。。 \(2^x mod(15)\) を書き込む量子ビットは mod(15) のラップアラウンドを実現するので 4 量子ビットになります。

\(x\) を入れる量子ビットを で重ね合わせした直後の状態ベクトルは、見やすく正方形に並べると次のようになります。

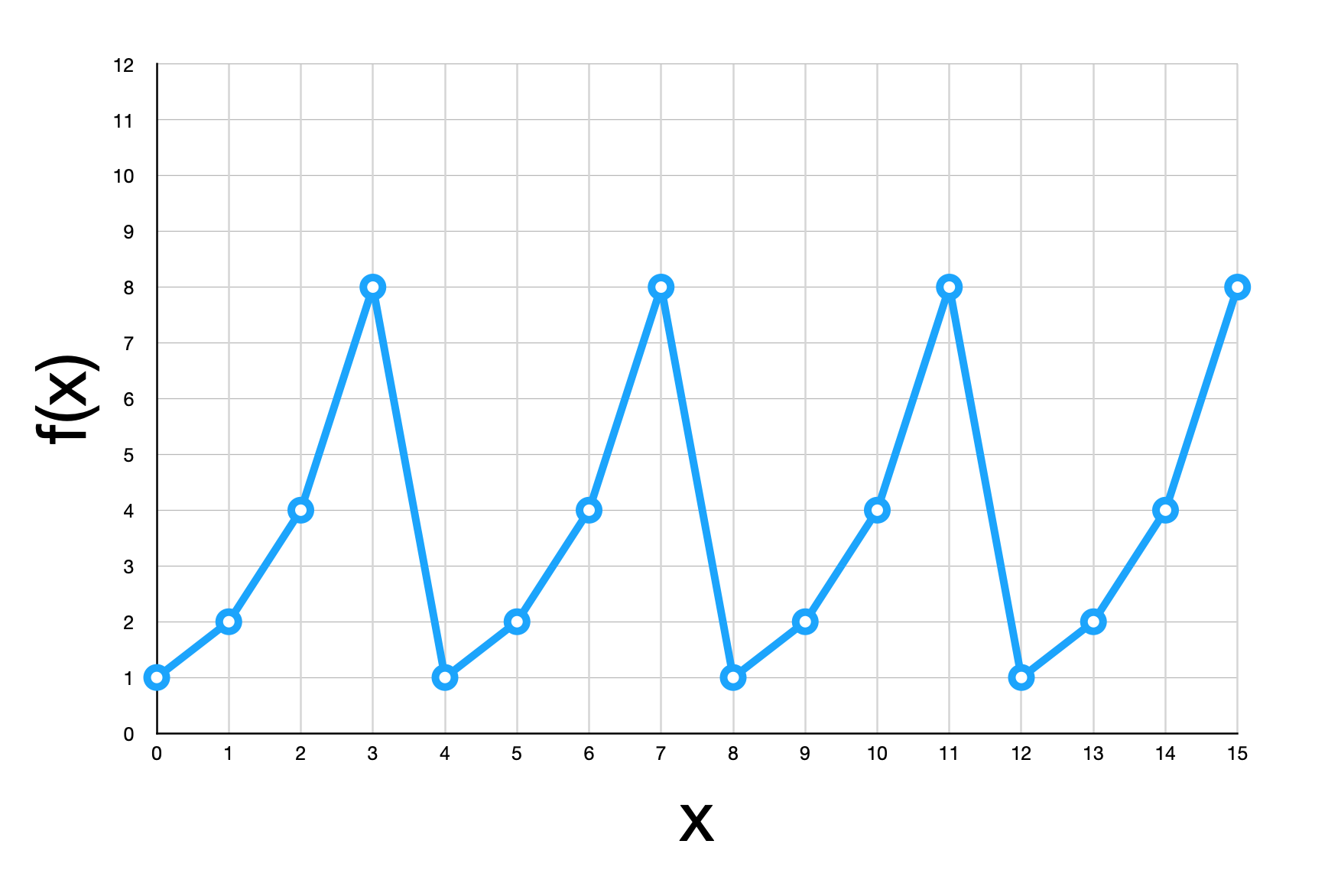
\(f(x) = 2^x mod(15)\) の値は列方向 (縦方向) に読みます。 \(|1\rangle\) や \(|17\rangle\) などに確率が散らばっていますが、測定すると \(f(x)\) は 100% の確率で 1 となります。 これは \(f(x)\) を \(|1\rangle\) に初期化したので当然です。 x の値は行方向 (横方向) に読みます。 で重ね合わせを作ったので、x の値は 0 から 15 までそれぞれ 6.25% の等しい重みを持ちます。

回路の次のブロックでは、条件つきの左シフト \(mod(15)\) を計算します。 \(x\) の最下位ビットが 1 の場合、\(f(x)\) の各ビットを左シフトすることで 2 倍します。 そして最上位ビットを最下位ビットにラップアラウンドすることで \(mod(15)\) します。 このとき状態ベクトルは次の状態になり、\(x\) の最下位ビットが 1 の場合だけ (= \(x\) が奇数の場合だけ) \(f(x)\) が 2 倍されたことが分かります。

回路の最後のブロックでは、同様に条件つきの左 2 ビットシフト \(mod(15)\) を計算します。 \(x\) の最下位から 2 ビット目が 1 の場合だけ、左 2 ビットシフトつまり 4 倍して \(mod(15)\) を書き込みます。 この時、状態ベクトルは次の状態になり、\(x\) の最下位から 2 ビット目が 1 の場合だけ f(x) が 4 倍されていることが分かります。

これで本当に \(2^x mod(15)\) がすべての \(x\) について計算できているのでしょうか？ 確率が 0 でない振幅の並びをよーく見てみると、これは最初のグラフを 90 度回転したものとまったく同じ位置にプロットされていることが分かります。 たしかに、状態ベクトルに \(2^x mod(15)\) を重ね合わせとして書き込むことができました! あとはこれを QFT にかけて、反復パターンを取り出すだけです。