QPU 命令その 1

X ゲート (量子 NOT)

演算ペアの入れ替え

X ゲート は従来の NOT 演算に似た働きをします。 NOT 演算は、0 に適用するとビットが反転して 1 になり、逆に 1 に適用すると 0 になるのでした。つまり、NOT 演算は "0 と 1 を入れ替える" という働きをします。

  • NOT 0 1
  • NOT 1 0

は NOT 演算の量子版で、量子ビットの \(|0\rangle\) と \(|1\rangle\) を入れ替えます。 図で表すと、次のような "円の入れ替え" の働きをします。

X ゲートを回路に置いて、\(|0\rangle\) と \(|1\rangle\) が入れ替わることを確認しましょう。

が従来の NOT 演算と異なるのは、重ね合わせ状態にある量子ビットに作用できる点です。 たとえば、次の \(|0\rangle\) と \(|1\rangle\) の重ね合わせ状態にある量子ビットを考えましょう。

これに を適用すると、\(|0\rangle\) と \(|1\rangle\) の内容を交換します。 これはまさに、先ほど見た "\(|0\rangle\) と \(|1\rangle\) の入れ換え" という効果です。

を続けて 2 回適用するとどうなるでしょうか? 図から分かるように、 \(|0\rangle\) と \(|1\rangle\) が 2 度入れ替わることで元の状態に戻ります。 つまり、量子 NOT ゲートはそれ自身を打ち消す効果を持っています。数学ではこれを、「量子 NOT ゲートはそれ自身の逆演算である」と言います。

  • 重ね合わせ状態の量子ビットに を適用し、\(|0\rangle\) と \(|1\rangle\) が入れ替わることを確認しましょう。
  • を 2 回適用すると元に戻ることを確認しましょう

「X ゲート」の名前の由来は、量子ビット状態をブロッホ球で表すと量子 NOT ゲートは X 軸を中心とした回転操作の一種だからです。

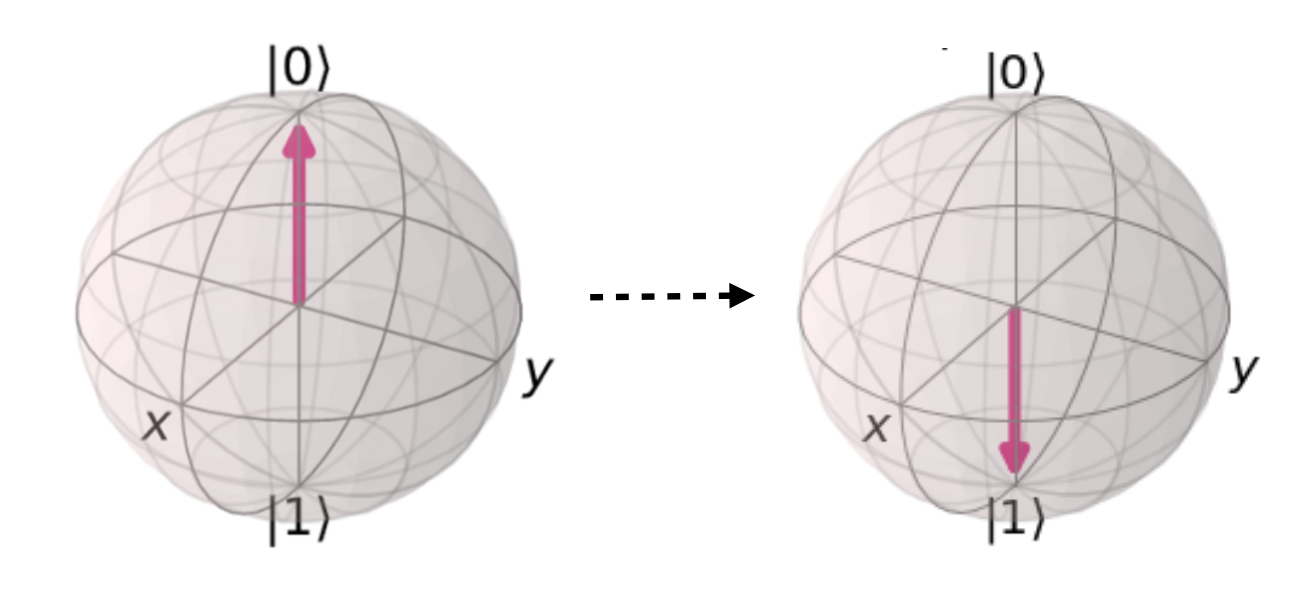
X ゲートは X 軸を中心に π (180度) 回転する操作 (画像クレジット: qiskit.org)

同様に、Y 軸で回転する Y ゲート 、Z 軸で回転する Z ゲート も存在します。さまざまなゲートの回転については、他のゲートを学んだ後で詳しく説明します。