\(a^x\,mod(N)\) の計算

ショアの因数分解回路の具体的な実装に移る前に、計算の流れ全体を押さえておきましょう。 ショアのアルゴリズムの量子部分は、大きく分けて次の 2 ステップからなります。

• \(f(x) = a^x\,mod(N)\) を計算する
• \(f(x)\) の周期 \(r\) を求める

今回はこのうち、最初の \(f(x) = a^x\,mod(N)\) を重ね合わせで計算する部分を見ていきます。

\(f(x) = a^x\,mod(N)\) を計算する

\(f(x) = a^x\,mod(N)\) を計算するために、まずは変数 \(x\) を回路上に準備します。 たとえば \(x\) が 0 から 15 までの値を取るなら、\(x\) の値は 4 ビットで表せます。 \(|0\rangle\) で初期化した 4 つの量子ビットに を適用することで、0, 1, ..., 15 を重ね合わせた \(x\) を作ることができます。

次にこの重ね合わせた \(x\) の上で \(f(x) = a^x\, mod(N)\) を計算し、結果を別の量子ビットに書き込んでいきます。 \(x\) を入れた 4 量子ビットの下に、計算結果を入れるための量子ビットを 4 つ確保しておくこととします。 \(x\) が 0 の時 \(f(0) = 1\) なので、この量子ビットは \(|1\rangle\) で初期化しておきます。

ここで、実装がブラックボックスなゲート U というものを考えます。 この U を計算結果用の量子ビットに適用すると、現在の値を \(a\) 倍し、\(mod(N)\) した値を書き込んでくれるものとします。 目的は \(a^x\, mod(N)\) を計算することですから、U を \(x\) 回置けば計算結果用の量子ビットに \(a \times a \times \dots \times a\,mod(N) = a^x\, mod(N)\) の値が残ります。

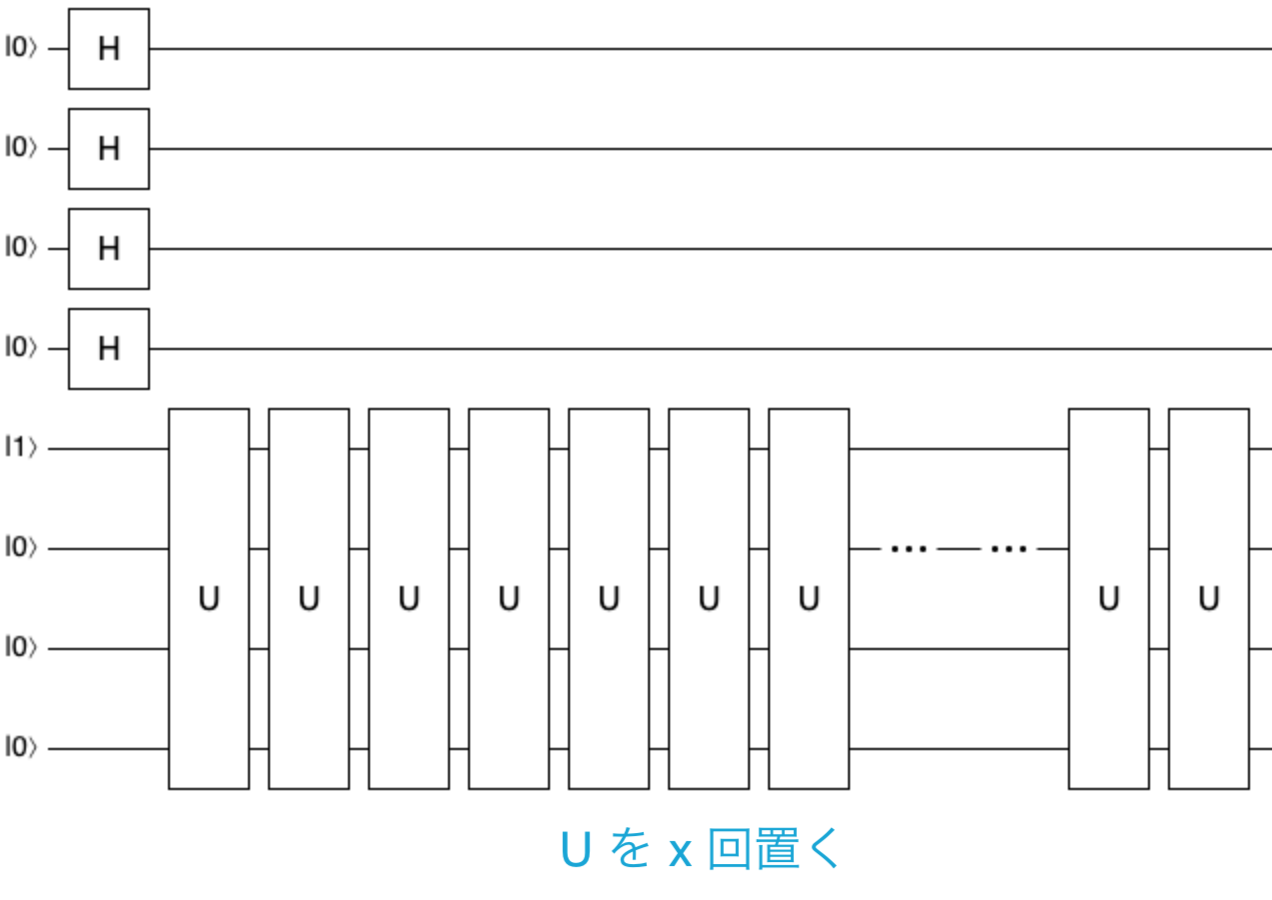
U を何回置くかという \(x\) の値は上の 4 量子ビットにエンコードされているので、これを使います。 \(x\) の値は二進数で量子ビットに格納されており、最下位ビットが \(2^0 = 1\)、次が \(2^1 = 2\)、... となっています。 このことから、制御付きの U を次のように置けば U を \(x\) 回適用したことになります。

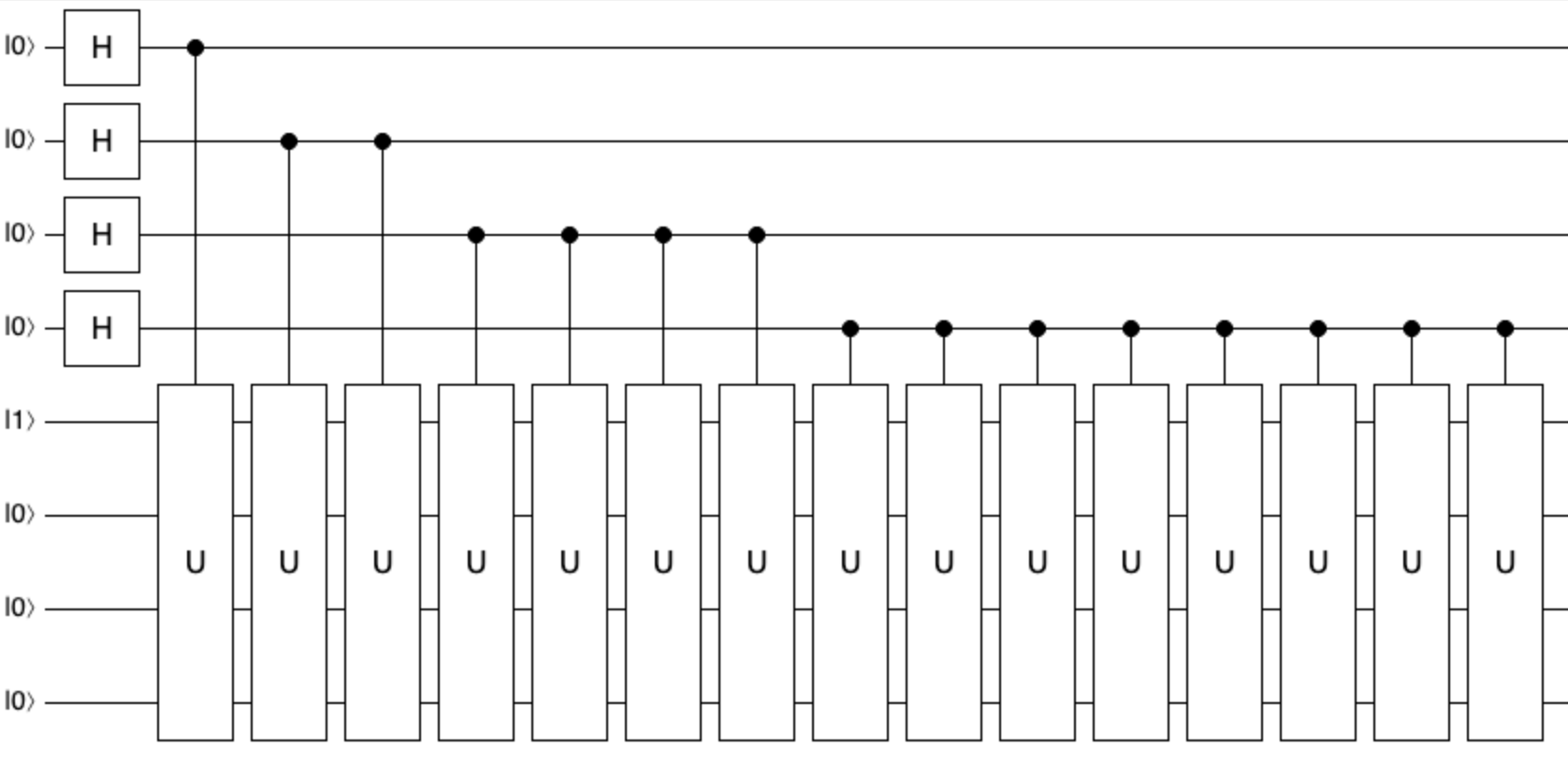
こうすれば、\(x\) の値は 0 〜 15 の重ね合わせであったため、計算結果用の 4 量子ビットにも \(a^x\, mod(N)\) の値の重ね合わせが書き込まれます。

量子位相推定との関係

この回路の形を見て、何か思い出した人はいるでしょうか？ そう、量子位相推定回路の前半とそっくりです。 実際にショアの因数分解回路の後半では、\(f(x)\) の周期 \(r\) を求めるために QFT を実行します。 こうなると量子位相推定回路と完全に一緒で、実際に数学的にも同等な回路です。

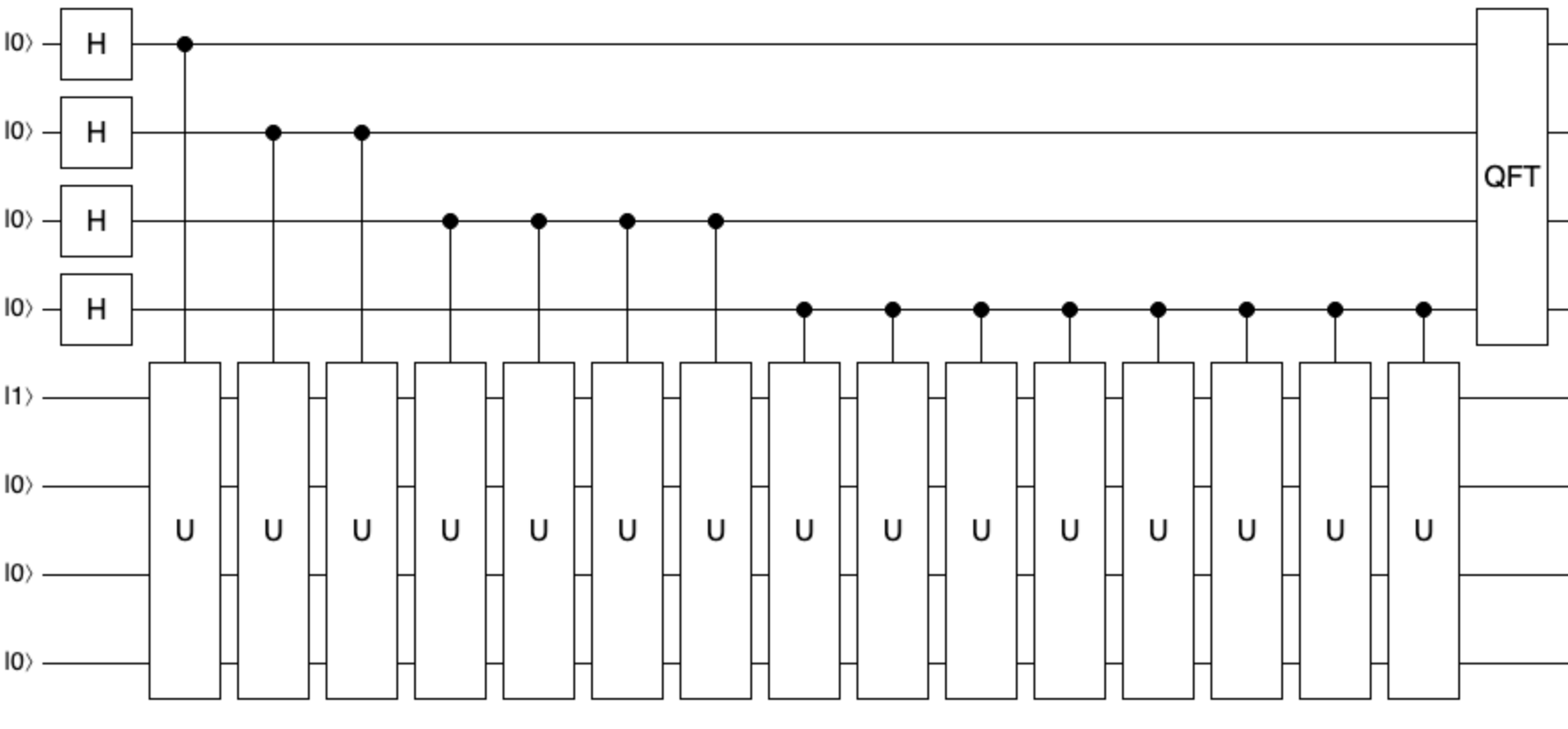
なぜ周期 \(r\) を求める問題が最終的に固有位相の推定問題になるかは、少し難しい数学が必要なので割愛します興味のある読者は、Qiskit チュートリアル 「ショアのアルゴリズム」を参照してください。https://qiskit.org/textbook/ja/ch-algorithms/shor.html。固有位相の概念を使わなくても、残る QFT 部分を含めショアのアルゴリズムの理解には問題ありません。 QFT の部分は次回に説明します。

まとめ

\(a\,mod(N)\) を計算できるゲート U があったときに \(a^x\, mod(N)\) を計算する回路を見ました。 この回路を実行すると、量子ビット上に前回見たような周期関数の値が重ね合わせとして書き込まれます。

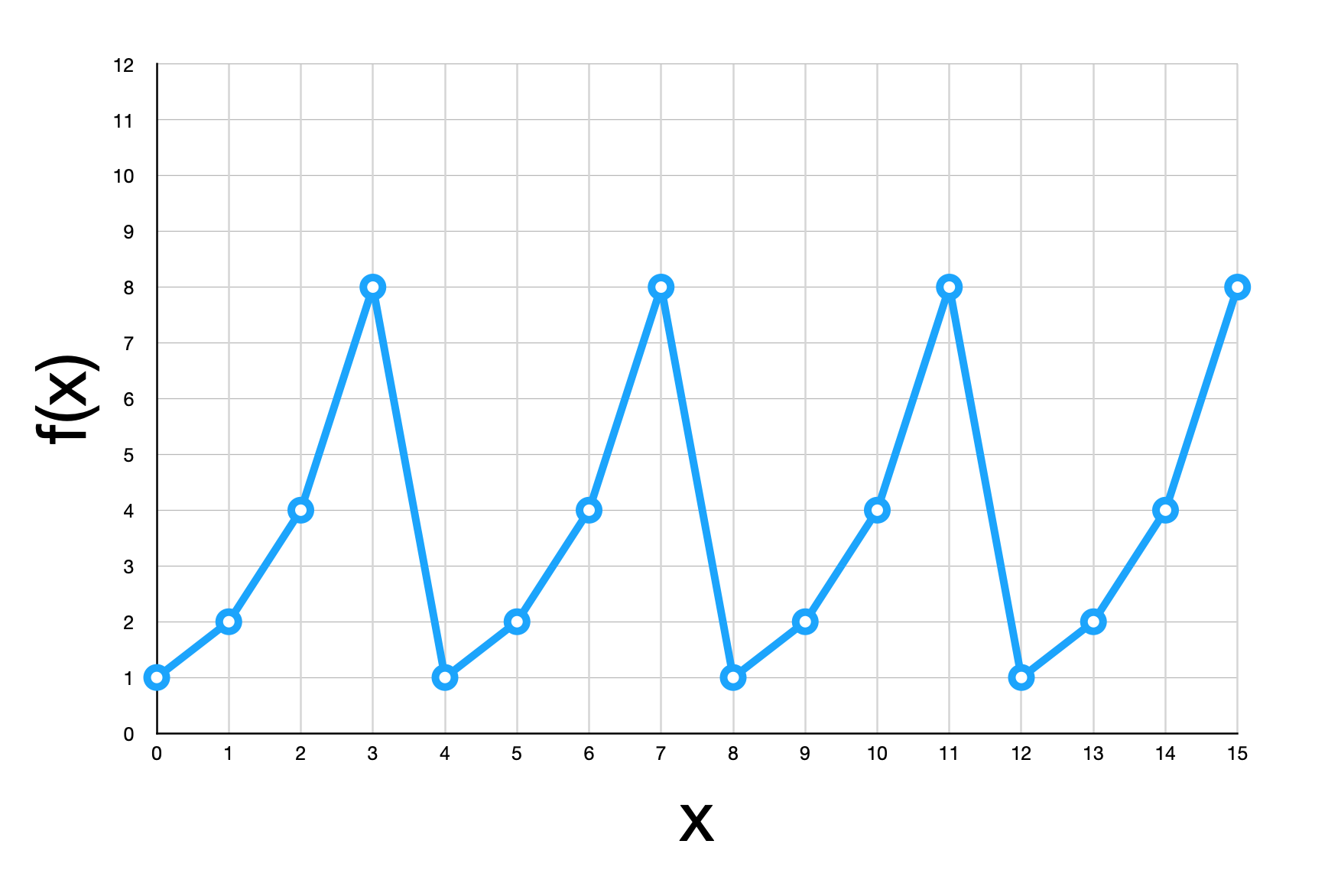
ここから周期 \(r\) を取り出すには、パターンを取り出すツールであるおなじみ QFT を使います。